Кубик 4 на 4 паритеты: Паритеты 4х4 — Кубик Рубика 4х4 решение паритетов в картинках
Содержание
Как собрать кубик Рубика 4 на 4
Сборка кубика Рубика 4 на 4 может показаться сложной, но на самом деле это не совсем так. Суть сборки кубика 4 на 4 состоит в том, чтобы привести куб к состоянию, когда он не отличается от кубика 3 на 3. Как собрать кубик Рубика 4х4 — Вы узнаете в этой статье.
Язык формул
Чтобы понимать формулы, необходимо знать все обозначения, которые в этих формулах упоминаются. Если Вы умеете собирать куб 3 на 3, это не составит для Вас труда, ведь к стандартным обозначениям добавляются еще обозначения поворотов внутренних граней.
- F (front) – фронтальная грань
- B (back) — задняя грань
- L (left) — левая грань
- R (right) — правая грань
- U (up) — верхняя грань
- D (down) – нижняя грань
- f – внутренняя фронтальная грань
- b — внутренняя задняя
- l — внутренняя левая
- r — внутренняя правая
- u – внутренняя верхняя
- d – внутренняя нижняя
- (Ff) — две фронтальные грани
- (Bb) — две задние грани
- (Ll) — две левые грани
- (Rr) — две правые грани
- (Uu) — две верхние грани
- (Dd) — две нижние грани
- F’, r’, (Ll)’ .
.. – поворот против чаcовой стрелки - F2, r2, (Ll)2 … — поворот 2 раза (180 градусов)
.. – поворот против чаcовой стрелкиУ нас в каталоге магазина легко выбрать кубик рубика 4х4.
Шаг 1 – собираем центры
На первом шаге необходимо собрать центры кубика, так называемые «центральные четверки» (изображение 1). У кубика 4 на 4 нет четкого, закрепленного центра, а это значит, что располагать правильно центры относительно друг друга нужно самостоятельно.
Правильное расположение цветов – изображение 2, придерживайтесь его. Вращением внешних граней вы не нарушите положение центральных элементов. На этом шаге нужна только 1 формула – изображение 3: (Rr) U (Rr)’ U (Rr) U2 (Rr)’ U2. Перед тем, как применить ее, подготовьте кубик: вращайте внешние грани чтобы спозиционировать элементы центров, которые Вы хотите поменять местами. Формулу примените чтобы поменять элементы местами. При этом другие элементы центров не будут затронуты.
Изображение 1 Изображение 2 Изображение 3
Шаг 2 – собираем ребра
На втором шаге необходимо собрать пары ребер кубика (изображение 4).
Вращайте внешние грани так, чтобы при вращении двух правых или двух левых граней реберные элементы кубика совмещались. На изображениях далее показаны исходные позиции перед применением формул, а крестиком отмечены реберные пары, которые не состыкованы.
Выполнение формул не затронет собранные ребра и центры. Помните, что на рисунках считается что синий – это передняя грань, а красный – верхняя.
(Ll)’ U’ R U (Ll) — изображение 5
(Ll)’ U’ R2 U (Ll) — изображение 6
(Ll)’ U’ R’ U (Ll) — изображение 7
Изображение 4 Изображение 5 Изображение 6 Изображение 7
Шаг 3 – паритеты
После шагов 1 и 2 у вас собрался кубик Рубика 4 на 4, который внешне не отличается от куба 3 на 3. Вращая только внешние грани по формулам сборки кубика 3 на 3 вы сможете быстро собрать кубик Рубика 4 на 4.
Действия не будут вызывать у Вас затруднения до последнего слоя.
На этом этапе Вам могут попасться паритеты.
Паритеты – это положения на кубиках 4 на 4 (и 5 на 5, и выше), которые невозможны в кубиках 3 на 3. На изображениях приведены все возможные случаи паритетов на кубике 4 на 4 и формулы для их сборки и решения.
Заметим, что для ситуаций 19-22 применяется одна и та же формула. Это не страшно, если вдруг после ее применения верхний
слой кубика немного разрушится — паритет у вас будет решен, так что собирайте дальше верхний слой по формулам 3х3.
Как собрать кубик Рубика 4х4: пошаговая инструкция для новичка
Для того, чтобы собрать кубик Рубика 4х4, нужно знать, как собирается кубик 3х3. Если вы ещё не умеете собирать его, можете глянуть подробное обучение для начинающих на нашем сайте.
Конечно, есть и такие способы сборки кубика 4х4, в которых не используется этап 3х3. Но такие способы не используются почти никем, так как они намного медленнее и сложнее для изучения. Все «новичковые» и профессиональные методы на данный момент используют именно приведение к кубику 3х3.
Иное название такого приведения – редукция.
Тот способ, которому мы научим вас, очень близок по структуре к профессиональным методам. Это значит, что он быстрее других «новичковых» методов, а если вы захотите выучить профессиональные методы, вам будет проще это сделать.
Конечно, по нашей схеме вы не научитесь собирать за 20 секунд, как профессионалы. Но наше обучение — отличный вариант для того, чтобы сделать свои первые шаги в мире спидкубинга. И этого метода будет достаточно, чтобы выступать на соревнованиях!
Первый этап. Сборка центров
Сборка кубика 4х4 начинается с центров (картинка 1). Для начала соберём один из них, например белый. Этот этап легко выполнить даже без алгоритмов.
Картинка 1
Затем нужно собрать противоположный центр – жёлтый. Собирать его нужно именно на противоположной грани, иначе в конце кубик не соберётся. Для этого нужно использовать две простых формулы:
- Поднять два слоя справа (картинка 2), верхнюю грань влево (один слой) и опустить два слоя справа.
- Поднять два слоя справа, повернуть верхнюю грань два раза, опустить два слоя справа.
Картинка 2
Сначала сделаем жёлтую полоску на боковых гранях – два жёлтых центра, стоящие рядом. Расположим их так, как показано на картинке 3, при этом держим белый центр внизу. Делаем второй алгоритм. Если наверху оказалось только 2 жёлтых центра, делаем полоску ещё раз, ставим её в то же место, полоску на верхней грани ставим над плоской на фронтальной грани и делаем второй алгоритм. Если наверху оказалось 3 жёлтых центра, ставим место, куда должен встать оставшийся центр сзади слева на верхней грани, а сам нужный центр – снизу справа на фронтальной грани. После этого делаем первый алгоритм.
Картинка 3
Теперь нужно взять кубик белой гранью слева, жёлтой справа. На той грани, что оказалась сверху, собираем зелёный центр, это также делается интуитивно – соберите две полоски и соедините их. Затем перехватываем кубик так, чтобы этот центр оказался на задней грани и собираем сверху оранжевый центр.
Для этого используем ту же методику, что и для жёлтого, при этом если какие-либо оранжевые центры находятся на нижней грани, перемещаем их на фронтальную теми же алгоритмами. Если же центр уже собран, но на другой грани – представьте, что это просто две полоски. После того, как оранжевый центр собран, перехватите кубик ещё раз и соберите на верхней грани синий центр. Тут может возникнуть ситуация, при которой на одной грани есть полоска, а на другой нет. В таком случае нужно сделать второй алгоритм, при этом держать готовую полоску справа, на какой грани она бы ни находилась. То же самое стоит сделать если на верхней грани есть лишь один элемент синего цвета. Красный центр на фронтальной грани соберётся сам.
Второй этап. Сборка рёбер
Теперь нужно собрать рёбра. На кубике 4х4 каждое ребро состоит из двух маленьких рёбер (картинка 4).
Картинка 4
Для того чтобы собрать такое ребро, нужно поставить два маленьких ребра друг напротив друга (картинка 5).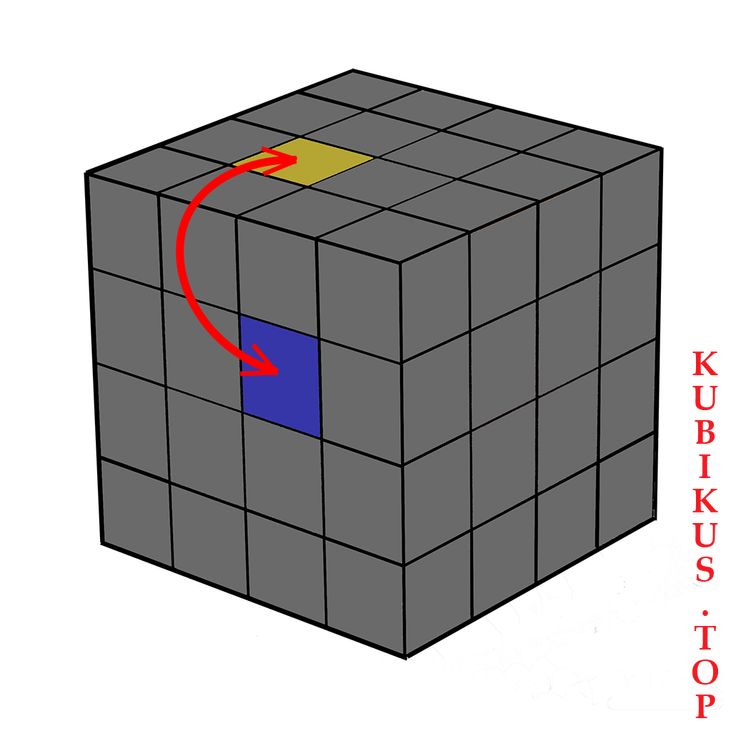
После этого делаем следующий алгоритм: два слоя верхней грани вправо, правую грань вверх (везде, где не указано, что слоя два, делаем движение одним слоем), верхнюю влево, правую вниз, фронтальную по часовой стрелке, правую вниз, фронтальную против часовой стрелки, правую вверх, два слоя верхней грани влево. Затем ищем новое ребро и делаем тот же алгоритм. Повторяйте эти действия до тех пор, пока не соберутся все рёбра на кубике.
Картинка 5
Третий этап. Сборка обычного кубика Рубика
После этого осталось собрать кубик так, будто это кубик 3х3. Но есть две особенности. Их называют паритетами. Первый паритет может возникнуть при сборке креста верхнего слоя. Если верно ориентированы три ребра, или лишь одно, нужно сделать довольно длинный алгоритм. Но не пугайтесь, после небольшой практики вы легко его запомните. Для этого выучим несколько простых обозначений. Верхняя грань – U, правая грань – R, левая грань – L. Так обозначаются движения по часовой стрелке одного слоя.
Если нужно сделать движение двумя слоями, добавляется маленькая буква w, например Rw, Uw, Lw. Есои нужно повернуть грань два раза – дописывают цифру 2, а если против часовой стрелки – дописывают символ ‘. Теперь можно выучить алгоритм: делаем Rw U2, перехватываем кубик так, чтобы верхняя грань оказалась сзади и продолжаем. Rw U2 Rw U2 Rw’ U2 Lw U2 Rw’ U2 Rw U2 Rw’ U2 Rw’.
Также существует второй паритет – его вы увидите уже на предпоследнем этапе – будет поменяно местами лишь два угла. На самом деле технически это вызвано тем, что местами меняются два ребра. Для того чтобы собрать кубик, мы делаем следующий алгоритм: Rw2 R2 U2 Rw2 R2 Uw2 Rw2 R2 Uw2. После этого продолжаем сборку кубика с этапа сборки правильного креста на верхнем слое.
Как собрать кубик 4х4 – Месть Рубика
Введение
Кубик 4x4x4 — следующая головоломка в серии кубиков Рубика, известная как
Месть Рубика . Хотя кажется, что это намного сложнее, чем знаменитая 3×3, решение мести Рубика 4×4 очень похоже на нее и требует изучения лишь нескольких дополнительных алгоритмов.
Сначала научитесь собирать кубик 3×3
Чтобы собрать кубик 4х4, вам нужно сначала узнать, как собрать кубик Рубика 3х3. Если вы не знакомы с решением или не помните его, просмотрите решение 3×3, прежде чем продолжить. Лучше всего освоить решение 3×3, прежде чем переходить на 4×4, хотя это и не обязательно.
Переместить обозначения
Те же правила записи ходов применимы и к кубу 4×4, с двумя отличиями:
1. Строчные буквы означают поворот 2 слоев соответствующей грани.
2. «2» перед буквой грани (например, 2R) означает перемещение только внутреннего слоя соответствующей грани.
[ r ]
[ 2R ]
Механика
Механика 4х4 немного отличается от классического кубика Рубика 3х3. Нет единой центральной части, а есть 4 центральные части каждого цвета; поэтому они не фиксируются в своих положениях.
Нет фиксированных центральных частей: В кубе 4×4 нет фиксированных центральных частей, что означает, что эти центральные части могут перемещаться по кубу и заменять друг друга местами (в отличие от 3×3, где желтые всегда остаются напротив белых, для пример). Это означает, что мы не можем определить цветовую схему куба, глядя на центральные части (мы будем использовать память или угловые части). Как уже упоминалось, есть 4 центральных элемента для каждого цвета. Для 4 центральных частей, собранных вместе, мы называем центральный блок . (На изображении: пример решенного красного центрального блока)
Несколько граней: каждая грань в кубе 4×4 имеет идентичную кромку вокруг куба, то есть существует 2 кромки каждого типа (например, 2 желто-красных кромки). На втором этапе мы собираемся соединить их вместе. Для двух одинаковых краев, соединенных вместе, мы называем краевым блоком . (На изображении: пример парного красно-синего реберного блока)
Решение
Шаг 1 Шаг 2 Шаг 3 Шаг 4
Шаг 1: Решение центральных частей
Первый шаг заключается в том, чтобы полностью собрать 6 центральных блоков, всего 24 элемента.
Мы начнем с решения 1-го центрального блока . Удачи!
В этом руководстве для начала я выбрал желтый цвет . Собрать первый центральный блок должно быть довольно легко, так как нет деталей, которые нужно сохранять. Вот как вы должны подойти к этому: начните с сопоставления 2 центральных частей рядом друг с другом и поднесите к ним 3-ю и 4-ю части.
Пример: собираем 4-й центральный элемент.
Решение:[ r’ F r ]
Объяснение: , выполняя движение r’ , вы опустите верхнюю правую желтую центральную часть на верхней грани на лицевую сторону (теперь она будет смежно с центральной частью на лицевой стороне), затем Переместите F , чтобы выровнять обе детали по правой стороне лицевой стороны, и, наконец, переместите r , чтобы вывести их обе вверх на верхнюю грань и сформировать полный желтый центральный блок.
Если бы желтая деталь на передней панели находилась в другом положении на передней панели (из 4 возможных положений), вы могли бы просто сделать несколько F-поворотов, чтобы отрегулировать ее.
То же самое касается верхней грани.
Я сделал инструкции для этой части короткими, так как это интуитивно понятная часть. Просто найдите время, чтобы попрактиковаться в движениях куба 4×4, и вскоре вы освоите способность интуитивно создавать центральные блоки.
2-й центральный блок: Второй центральный блок, который нужно решить, должен быть , противоположный цвету по сравнению с предыдущим, который мы только что решили: поскольку мы решили решить только желтый центральный блок, теперь нам нужно решить белый центральный блок (это относится только к исходным кубикам цветовой схемы! Там, где желтый находится напротив к белому, красный к оранжевому и синий к зеленому.)
Переверните куб так, чтобы желтый центральный блок оказался внизу. Способ решения белого центрального блока заключается в перемещении белых центральных частей по одной (или попарно) на верхнюю грань (конечно, не повреждая решенный центральный блок внизу).
Поскольку сохраняются только нижняя и верхняя части посередине, вы можете свободно переворачивать: F / B / R / L слоев.
Способ «загрузки» центральной части боковой грани (F / B / R / L) в верхнюю грань заключается в использовании следующих движений:
Пример: загрузка 2 белых центральных частей с грани F (одинаково для всех граней).
Решение: [ r’ F2 r ]
Объяснение: так как мы должны сохранить центральные части внизу, просто сделать движение вправо/влево недостаточно. Поэтому делаем r’ переместите и снимите небелые центральные фигуры сверху на поверхность F, затем поменяйте их местами с 2 белыми фигурами, выполнив F2 . (В данный момент на задней стороне есть 2 желтые фигуры, которые вернутся в исходное положение на следующем ходу). Теперь мы, наконец, изменим ход r’, сделав ход r . Белые фигуры теперь правильно расположены на верхней грани, а все желтые фигуры на нижней остались невредимыми.
Это важная идея для понимания решения 4×4. Это как « Лифт «движение, мы спускаем «лифт» к фигурам, которые мы хотим переместить, «загружаем» фигуры в «лифт» и поднимаем их вверх в решенное положение.
Таким образом, мы можем позиционировать фигуры, пока сохранение уже решенных частей.
Когда 3 центральных элемента находятся сверху:
Здесь реализована та же идея: мы также воспользуемся идеей лифта. На самом деле алгоритм почти аналогичен
Решение: [ r’ F r ]
Единственная разница в том, что нам нужно сделать только один F-поворот, потому что одна белая фигура уже была «внутри» лифта.
Если 3 белые части сверху или часть на лицевой стороне расположены иначе, чем в примере, все, что вам нужно сделать, это всего лишь несколько поворотов U / F, чтобы отрегулировать их, как на изображении, и решить.
3-й центральный блок: мы можем выбрать любой из оставшихся четырех цветов в качестве третьего блока для решения.
В этом руководстве я выбрал красный .
Лучше всего повернуть (перевернуть) куб так, чтобы решенные центральные блоки (желтый и белый) оказались на правой и левой гранях.
Сделайте несколько ходов r/r’ и U/F/B/D , чтобы сформировать 2 соседние красные фигуры.
Поверните (переверните) куб так, чтобы они появились на верхней грани (желтые и белые по-прежнему на правой и левой гранях). Затем сделайте несколько разворотов, если необходимо, чтобы выровнять 2 красных центральных элемента на левой стороне верхней грани (см. изображение для пояснений левой/правой внутренней стороны) (может быть и правая сторона, я лично привык к левой, так как я правша), как в примере ниже (правое изображение):
Пример: образует 2 соседних красных элемента.
Решение: [ U’r U ]
Объяснение: мы сделаем ход U’ (поэтому, когда мы сделаем ход r, две красные фигуры станут рядом друг с другом, а не по диагонали), затем мы сделаем ход r движение, чтобы соединить 2 красные центральные фигуры, и, наконец, мы сделаем движение U , чтобы выровнять их обе слева.
Решение оставшихся 2 частей: Лучший способ сделать это — расположить одну красную центральную часть с левой стороны (внутренняя левая) куба, а вторую — с правой стороны, а затем сделать движение вправо/влево, чтобы соединить их в пары.
В следующем примере обе оставшиеся части находятся на правой стороне (внутренней правой) куба (одна находится на верхней грани):
Решение: [ F2 r’ F r ]
Объяснение: Сначала мы сделаем ход F2 , чтобы переместить одну фигуру в левую сторону (так что следующий ход r’ не повлияет на нее, и она соединится с фигурой, которая в данный момент находится сверху) (The Причина, по которой мы делаем F2, а не F’, заключается в том, что на следующем ходу мы хотим, чтобы они образовали пары рядом друг с другом, а не по диагонали). Тогда мы сделаем r’ ход, чтобы соединить фигуры в пары. Теперь сделаем движение F , чтобы выровнять обе части по правой стороне лицевой стороны. Наконец, мы сделаем ход r , чтобы собрать их в окончательное положение на верхней грани, чтобы все 4 красных центральных элемента были полностью собраны.
*Приведенный выше пример применим ко всем возможным случаям, так как, выполняя движения «п/р» и «П/Б/Н/Н», вы можете расположить 2 оставшиеся центральные фигуры в одном и том же положении и решить таким же образом.
4-й центральный блок: Четвертый центральный блок, который нужно решить, имеет цвет, противоположный тому, который мы только что решили,
означает оранжевый (опять же, относится только к исходным кубам цветовой схемы, где оранжевый противоположен красному).
Сначала мы перевернем куб вверх дном, чтобы красный центр оказался на нижней грани (желтый и белый по-прежнему на левой и правой гранях). Нам нужно перенести все оранжевые центральные части на верхний слой. Надеюсь, некоторые из них уже есть.
Мы воспользуемся принципом «лифта», чтобы загрузить оранжевые элементы наверх, не повреждая красные элементы внизу. Вот пример того, как это делается:
Решение: [ r’ F’ r U ]
Объяснение: сначала мы сделаем ход r’ , чтобы снести «лифт» с неоранжевыми центральными частями наверху. Затем мы сделаем ход F’ , чтобы загрузить фигуру в лифт (правильно делать F’, а не F2, чтобы совпасть рядом с оранжевой фигурой сверху).
Затем мы сделаем движение r , чтобы поднять лифт обратно в решенное положение. Наконец мы сделаем U переместить, чтобы выровнять обе части по левой стороне центра (чтобы «освободить» лифт для следующих 2 частей).
Собираем оставшиеся 2 центральные детали: Лучший способ собрать оставшиеся 2 детали — перемещать по одной детали в верхний слой, используя принцип лифта:
Решение: [ r’ F r ]
(Если вы забыли, мы не можем просто сделать ход [r], потому что внизу есть красные центральные фигуры, которые нужно сохранить)
Объяснение: делаем ход r’ (снос «лифта»), затем делаем ход F , чтобы загрузить в него оранжевую фигуру, наконец делаем r переместите, чтобы загрузить оранжевую центральную часть в решенную позицию. (Примечание: опять же, используя принцип лифта, ни одна красная центральная часть или желто-белая часть не пострадала).
Теперь мы снова применим ту же самую идею для последней центральной части:
Решение: [ F2 r’ F r ]
Объяснение: Сначала мы сделаем F2 движение, чтобы расположить оранжевую фигуру на левой внутренней стороне куба (Мы делаем F2, а не F, потому что мы хотим, чтобы она совпадала по соседству с другой оранжевой фигурой, которая дальше пойдет вниз).
Затем мы делаем ход r’ (спуская лифт), затем ход F , чтобы загрузить обе фигуры в «лифт». Наконец, мы загрузим обе части с ходом r и решим весь оранжевый центральный блок.
5-й и 6-й центральные блоки: Последние 2 центральных блока решаются одновременно, так как при решении одного цвета другие цветные блоки автоматически окажутся в противоположном центре, который является единственным доступным центром.
Важно! Эти центры можно решить правильно, а неправильно . Давайте выберем зеленый цвет , чтобы узнать его правильное положение (из 2 доступных мест). Согласно исходной цветовой схеме, когда желтый цвет сверху, а красный цвет на лицевой стороне, зеленый должен быть на 9-м месте.0006 справа .
Переверните куб так, чтобы будущая зеленая грань оказалась сверху.
Решить эти последние 2 центра проще, чем кажется, и это делается, выполняя только ходы r2 и U/B.
1) Сначала возьмите 2 соседних зеленых элемента на верхний слой (скорее всего, он уже там) и выровняйте их по левому краю.
Вот как это сделать:
Поместите зеленую центральную часть с левой стороны, используя U ходов. Сделайте ход r2 и посмотрите, образовались ли 2 соседние зеленые фигуры на верхней грани. Если да то ставь U/U’ переместить, чтобы выровнять их обоих по левой стороне, и сделать еще r2 , чтобы развернуть и вернуть все на место.
Если после выполнения первого хода r2 у вас нет соседних зеленых цветов, переверните ход r2 и сделайте несколько ходов D (посмотрите на нижнюю грань, чтобы увидеть, сколько нужно), поэтому, когда вы снова сделаете еще один ход r2, зеленая часть будет перемещена вверх и совпадет с зеленой частью, которая уже там.
Пример: Нижняя грань выглядит так: (поворот x)
Решение: [ D’ r2 U’ r2 ]
В этом случае зеленой пары сверху уже нет (обозначения смотрите только на левом изображении).
Объяснение: сначала требуется ход D/D’ , поэтому следующий ход r2 сформирует соседнюю пару зеленых центров наверху.
Затем ход r2 , чтобы совместить 2 зеленые фигуры вместе (подъемник поднимается вверх), затем ход U’ , чтобы выровнять обе зеленые фигуры по левой стороне («выгрузка» из лифта). Наконец-то r2 переместить, чтобы перевернуть все остальные части на место (лифт опускается).
2) Соединяем две другие зеленые фигуры в верхнюю грань: Здесь есть два варианта: только одна часть внизу или обе части внизу.
Если одна деталь сверху: более легкий случай. Совместите зеленую центральную часть внизу с левой стороной нижней грани (с помощью D/D’) таким образом, чтобы к следующему ходу r2 она совпала со второй зеленой частью. Сделайте ход r2 и сопоставьте 2 зеленые центральные части. Затем просто сделайте движение D/D, чтобы выровнять обе части по правой стороне нижнего центра. Наконец, сделайте ход r2, чтобы загрузить обе фигуры наверх. Все зеленые фигуры собраны, а все синие фигуры находятся внизу (все центральные части собраны!)
Пример:
Решение: [D r2 D’ r2 ]
Если обе части находятся внизу: есть 2 возможных случая — смежные или диагональные друг к другу-
Диагональ: [ r2 D/D’ r2 ] .
Объяснение: сделайте ход r2 так, чтобы одна зеленая фишка поднялась вверх на верхний слой. Затем сделайте ход D/D’ , чтобы переместить оставшуюся зеленую фигуру внизу на второе доступное место с левой стороны, так что рядом соответствует второй фигуре, которая в настоящее время находится сверху, как только она вернется вниз на следующем ходу. Теперь сделайте ход r2 , чтобы опустить зеленую фигуру. Зеленые центральные части теперь расположены рядом друг с другом. Продолжайте в соответствии с приведенными ниже инструкциями для смежных случаев.
Смежный: [ r2 D2 r2 ] . Объяснение: выровняйте обе зеленые фигуры по левой стороне центральной области внизу (сделав D/D’ ходов), затем сделайте r2 9Ход 0007 (принцип лифта). Сделайте ход D2 , чтобы поместить обе зеленые фигуры в правую сторону (чтобы их можно было поднять вверх следующим ходом), и, наконец, измените ход r2 , чтобы переместить зеленые центры наверх. столкнитесь и полностью решите зеленый (и синий!) Центральный блок!.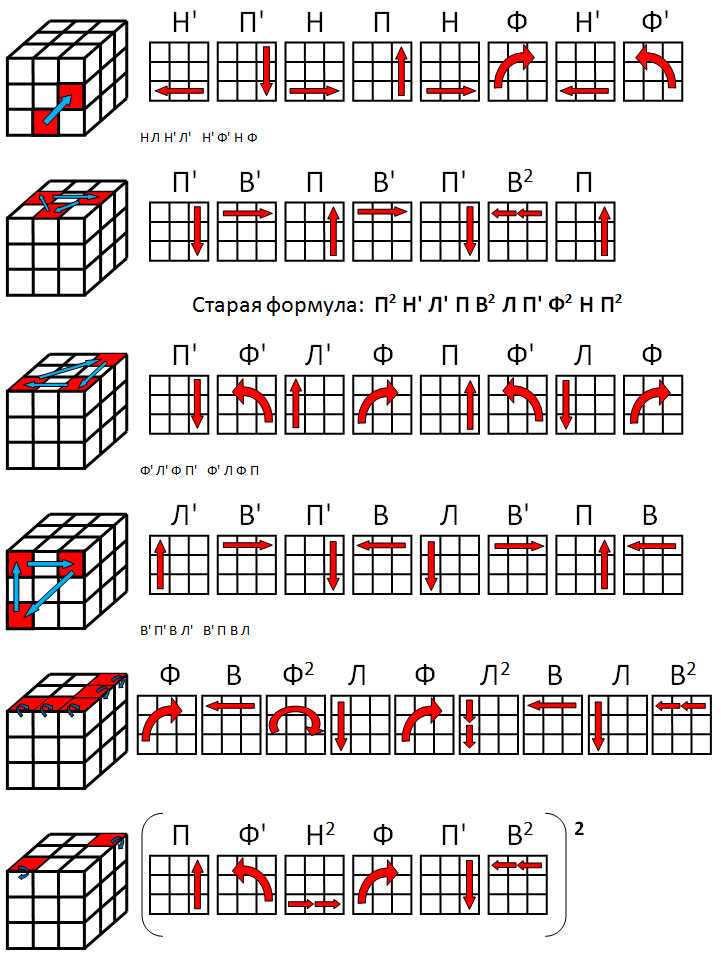
(см. пример ниже)
Пример: Нижняя часть выглядит так: (поворот x)
Решение: [ D’ r2 D2 r2 ]
Вот и все! Вы правильно собрали все 6 центральных блоков друг с другом. Я рекомендую вам остановиться на этом и попрактиковаться в сборке всех центральных блоков куба 4×4, пока вы не почувствуете себя комфортно, делая это интуитивно. Опытному сборщику кубика Рубика 3×3 не составит большого труда сделать это за день или два.
Шаг 2. Соединение всех кромок
Второй шаг заключается в объединении всех реберных частей с их идентичными близнецами на кубе 4×4 в реберных блоков . Нужно решить 12 краевых блоков, то есть всего 24 краевых элемента. На изображении справа вы можете увидеть пример двух бело-синих краев, соединенных вместе в один краевой блок (бело-синий краевой блок).
Перестановки краевых блоков вокруг куба совершенно бессмысленны на этом шаге.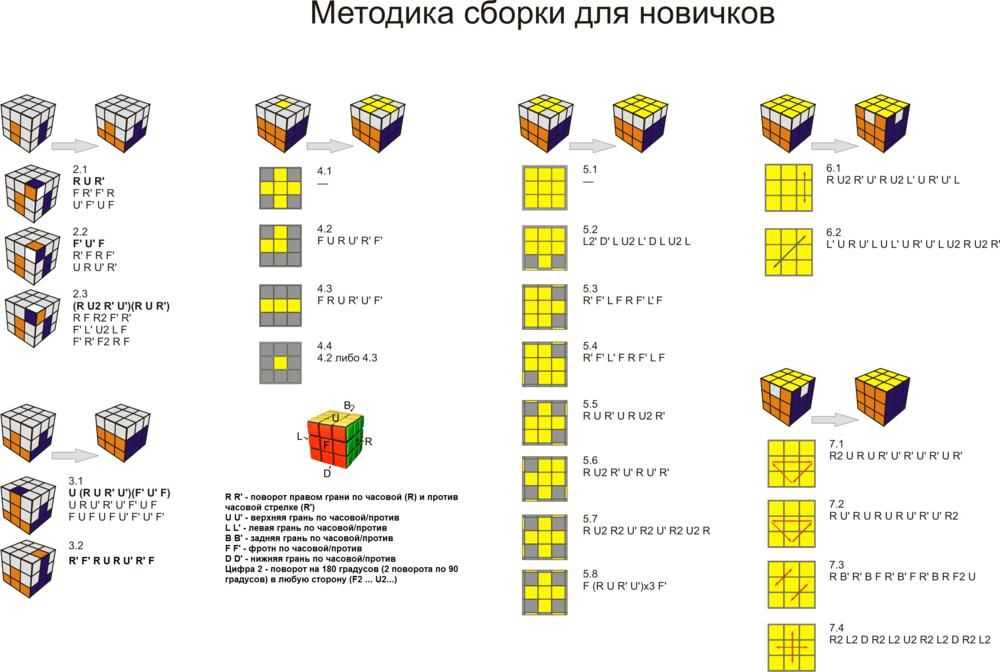
Решение первых 4 граничных блоков:
Здесь нужно объединить краевые части в блоки и сохранить их на верхней и нижней гранях (= 8 доступных мест. Мы начнем с 4 сверху). Помните, что вы можете делать любые ходы U/D/B/R/L/F, которые вы хотите, так как они не влияют на центральные фигуры.
Вот как это делается:
Найдите 2 одинаковых ребра, расположенных как на картинке, затем выполните следующий алгоритм:
Алгоритм: [ d R U R’ d’ ]
Этот алгоритм объединяет две крайние части в блок и сохраняет их на верхней грани, не повреждая центральную часть. Вот как: сделав ход d , две крайние фигуры соединится. Затем с помощью движения R сформированный краевой блок переместится вверх в верхний слой. Затем мы сделаем ход U/U’/U2 , чтобы закрепить блок наверху (чтобы он не опустился на следующем ходу — R’). Мы будем делать U/U’/U2 в соответствии с краевыми блоками вверху, если нет решенных краевых блоков, то это не имеет значения.
Если есть уже решенные блоки — мы хотим убедиться, что вместо этого их не сняли. Наконец мы сделаем R’ d’ , чтобы вернуть все остальные детали на место.
Используя этот метод, вы сможете быстро соединить и сохранить сверху/снизу первые 8 граничных блоков.
Как вставить крайние части в чехол выше?
Сначала поместите обе фигуры на одну грань, используя движения R2/L2/F2/B2 и движения U/D. Вот быстрый алгоритм перемещения 2 ребер в нужное положение (см. изображение):
Решение: [ L’ U L ]
С помощью этого простого алгоритма вы сможете правильно расположить 2 ребра, которые находятся на одной грани и имеют одинаковый цвет на общей грани (если нет, просто сделайте U-образный ход) в нужный корпус. Затем просто выполните соответствующий алгоритм [ d R U R’ d’ ] , и обе части будут объединены в пары и сохранены на верхней грани.
Используя описанный выше метод, вы сможете перевести все 8 первых пар ребер в положение простого регистра.
Начните с более легких ребер, которые уже находятся в этом положении. Чем меньше краевых кусочков останется, тем легче получится.
Если у вас уже есть парные ребра на сторонах куба (например, между передней и правой гранями), просто сделайте простой R/R’/L/L’, чтобы поместить его на верхний слой. Для парных рёбер на нижней просто сделайте двойное движение боковой грани, чтобы вывести её на верхнюю грань.
Пример: решение 4-го реберного блока.
Решение: [ L D’ L’ ] [ d’ L’ U L d ]
Объяснение: в этом примере видно, что уже сформировано 3 реберных блока, а четвертый разделен на грани F. В первых 3 ходах (первые скобки) мы двигаемся вокруг ребра внизу в «идеальный» случай, когда они оба находятся на боковых гранях с разными цветами на грани F, а затем просто решим это так, как описано выше (это тот же алгоритм, только слева — L вместо R)
Теперь все 4 крайних блока сверху сформированы, переходим к следующим:
Решение 5-8 реберных блоков:
Переверните куб вверх дном, чтобы все парные реберные блоки оказались на нижнем слое.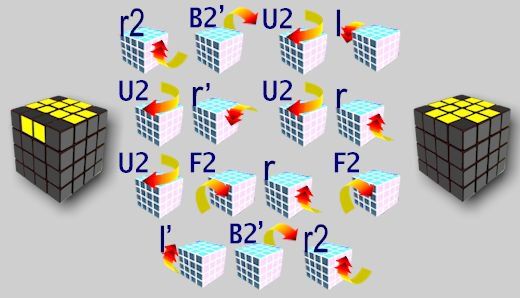
Теперь просто сделайте то же самое для следующих 4 пар ребер, используя те же алгоритмы и идеи, что и выше. Единственное отличие состоит в том, что для уже решенного реберного блока на боковых гранях: вместо использования перемещения R выполните – [R U R’], чтобы загрузить реберный блок в верхний слой, сохранив при этом нижние реберные блоки.
Пример: решить 8-ю пару.
Решение: [ d’ L’ U L d ]
(точно так же, как обсуждалось выше)
В этом примере формируются все краевые блоки внизу, а также формируются еще 3 блока на верхней грани. Осталось решить только одну. В нашем случае это будет красно-белая часть (вторая часть находится между передней и левой гранями). Решается точно так же, как показано в последнем примере.
После решения всех 8 краевых блоков на верхней/нижней гранях переходите к последним четырем:
Решение последних 4 граничных блоков:
Решение последних 4 граничных блоков немного сложнее, но очень короткое.
Здесь мы хотим, чтобы 2 части с двумя краями были с того же цвета на их общей стороне (как на изображении ниже).
Следующий алгоритм решает обе пары ребер одновременно, сохраняя при этом все остальные реберные блоки и центральные части:
Алгоритм: [ d R F’ U R’ F d’ ]
Это важный алгоритм; это алгоритм, который вам нужно запомнить, чтобы собрать кубик 4×4 наизусть. Потратьте некоторое время, чтобы получить его.
Используя этот алгоритм, вы решите все 4 последние пары ребер.
Если ребра не имеют одинакового цвета на их общей грани, как в примере ниже, используйте следующую последовательность движений:
Решение: [ R F’ U R’ F ]
Объяснение: этот алгоритм перевернет 2 ребра между передней и правой гранями. Теперь части будут совпадать для случая, описанного выше.
Если только одна пара ребер имеет одинаковый цвет на взаимной грани, а вторая пара не имеет (или даже не имеет одинаковых ребер), все равно выполнить алгоритм! Таким образом, вы решите 1 крайний блок из 4 оставшихся, и продолжайте, пока все 4 не будут решены.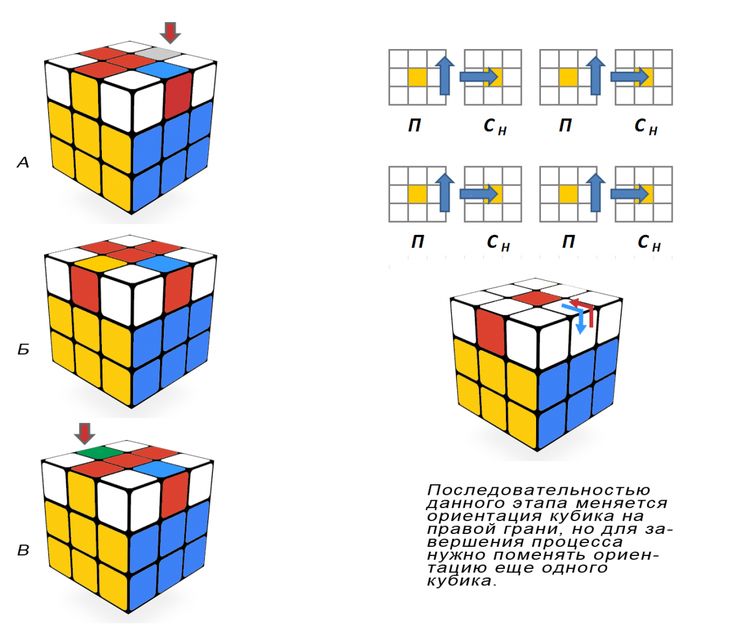
Вот и все! Теперь все краевые части уже должны быть спарены друг с другом. Вы можете заметить, что кубик выглядит как обычный кубик Рубика 3×3, и именно так вы собираетесь его сейчас собирать, как описано в инструкциях к следующему шагу.
Шаг 3. Сборка кубика Рубика 3×3 (до последнего слоя)
Кубик теперь действительно похож на обычный кубик Рубика 3x3x3! Считайте центральные блоки одной центральной частью, а краевые блоки — отдельными краевыми частями.
=
На изображениях выше вы можете видеть, что части 4×4 расположены
так же, как
, как куб 3×3.
Итак, с этого момента просто продолжайте собирать кубик, как это был кубик Рубика 3×3, до последнего слоя (непосредственно перед ориентацией последнего слоя).
Причина решения только до последнего слоя, а не завершения куба, заключается в том, что в кубе 4×4 могут возникнуть 2 особых случая, которые невозможны в кубе 3×3.
Их называют паритетами.
Шаг 4. Решение последнего уровня (четность OLL и PLL)
Вот возможные случаи, которые могут произойти при решении куба 4×4:
OLL паритет:
[ r U2 x r U2 r U2 r’ U2 l U2 r’ U2 r U2 r’ U2 r’ ]
Контроль четности PLL: (вид сверху)
[ 2R2 U2 2R2 u2 2R2 2U2 ]
Что такое четность OLL?
Четность OLL — это когда не ориентирован только один граничный блок. Это невозможный случай в обычном кубе 3х3. Этот случай решается по алгоритму выше. При необходимости важно выполнить алгоритм проверки четности OLL перед решением последнего слоя , потому что он не сохраняет позиции частей последнего слоя. Вероятность встретить четность OLL во время решения 4×4 составляет 50%.
Что такое четность PLL?
Четность PLL — это когда только 2 ребра остаются нерешенными, а остальная часть куба полностью собрана.
Этот случай также не может произойти на кубе 3×3 (причины ниже) и устраняется алгоритмом четности PLL. Алгоритм четности PLL сохраняет все фрагменты, кроме фрагментов переключенных ребер, и поэтому может использоваться в конце решения (после решения всех других фрагментов последнего слоя). Вероятность встретить четность PLL во время решения 4×4 составляет 50%.
Внимание! Вы можете столкнуться со странным случаем PLL, когда все фигуры собраны, но, например, 2 угла. Это из-за четности PLL. После применения алгоритма четности PLL это станет разрешимым случаем PLL.
Объяснение обозначений: Контроль четности PLL использует движение внутреннего слоя. Цифра «2», показанная перед указанной буквой грани, означает перемещение внутреннего слоя ее грани. Пример: [2R] = [r R’]. Перемещение «2R» можно выполнить, переместив оба слоя, выполнив r, а затем вернув грань R назад, выполнив R’. Перемещение «2R2» означает перемещение этого внутреннего слоя дважды. Вы можете увидеть примеры изображений во вступительном разделе выше.
Почему на кубах 4×4 происходит четность PLL, а на обычном кубе 3×3 это невозможно?
Причина в механике и математике кубика Рубика. Как вы знаете, переместить только 2 ребра, сохранив при этом все остальные, невозможно* (алгоритм U-perm затрагивает 3 ребра, что является минимально возможным). Переместить только одну фигуру заведомо невозможно (куда она пойдет без переключения другой фигурой?).
Таким образом, случай, когда необходимо поменять местами только 2 ребра, является невозможным для куба 3×3. Однако на кубе 4х4 не совсем 2 штуки, а 4 шт. , и 4 шт. необходимо переключить между — это возможный случай.
(* По крайней мере, не легальными ходами, единственный возможный способ сделать это — разобрать 2 части, разбив куб и собрав его неправильно (куб станет неразборным)
Те же правила применяются ко всем кубикам (3×3, 4×4, 5×5 и т.д..)
Как насчет паритета OLL?
Четность OLL происходит и в кубе 4×4 по тем же причинам.
Минимальное количество элементов ориентации при сохранении всех остальных элементов равно 2 (применяется для всех размеров кубов). Следовательно, в кубе 3х3 не может быть неориентированным только 1 ребро. В то время как в кубе 4×4 на самом деле это 2 разных ребра (хотя мы рассматриваем их как «один реберный блок»), которые это возможный случай.
Разобравшись с паритетами, продолжим и закончим сборку куба 4×4:
Если после выполнения шага 3 (решение куба до последнего слоя) вы заметили, что имеет место четность OLL — тогда примените алгоритм и продолжите решение последнего слоя, используя технику решения 3×3. При необходимости также примените алгоритм PLL.
Вот и все! Вы только что собрали Месть Рубика 4×4! Просто сохраняйте и тренируйтесь в сборке кубика 4×4, пока вы не сможете сделать это без использования этого руководства. Вы будете рады узнать, что для этого вам нужно запомнить всего 4 алгоритма (2 четности + 2 алгоритма из шага 2)! Поздравляем!
Надеюсь, вам понравилось собирать кубик Рубика 4×4 Месть Рубика .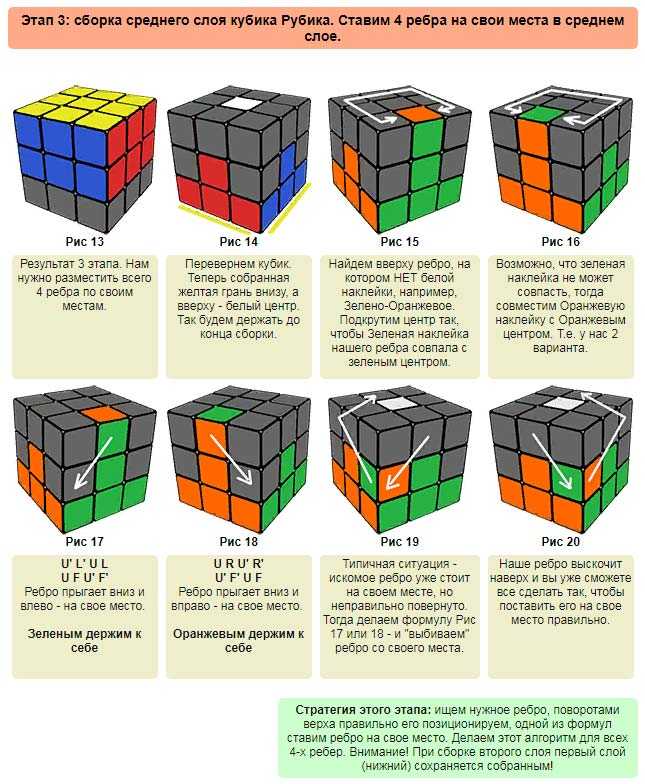
Приглашаем вас оставить комментарий на нашей странице в Facebook и написать о своем опыте решения проблемы.
Прочтите мое руководство по лучшим скоростным кубикам 4×4
Где я просматриваю лучшие на сегодняшний день кубики 4×4, текущие мировые рекорды, выбор лучших кубов и где их взять. Они намного быстрее и приятнее в разгадывании и стоят обычно меньше оригинальных рубиков 4х4.
Как быстро собрать куб 4x4x4
Как быстро собрать куб 4x4x4 — Сборка 3x3x3
Решение 3x3x3
Теория
Немного теории, но я думаю, что важно понимать, что сила центрового решения в первую очередь заключается в том, что вы превращаетесь в куб 3x3x3, где вы можете использовать все свои обычные приемы быстрого решения. Однако основным недостатком решения по центру являются две возникающие ошибки четности. Тем не менее, я думаю, что способность действительно использовать свои специализированные трюки 3×3 компенсирует эти
Забота о случаях четности
Итак, этот последний шаг — это страница о том, как я обрабатываю случаи четности.
Если вам нужна действительно хорошая страница, посетите страницу больших кубов Стефана Похманна. Также проверьте bigcubes.com.
Ниже показано, как я буду действовать в каждом случае, но есть много разных вариантов того, как с ними справиться.
OLL parity
Это четность, полученная путем решения центров таким образом, что перестановка ребер нечетна. Если скрембл имеет ребра в четной перестановке, и вы решаете центры в нечетном числе четвертей оборотов внутренней грани, вы получите четность ориентации. Если скремблирование начинается с ребер в нечетной перестановке, а центры решаются за четное число четвертей оборотов внутренней грани, то вы также получите четность.
Эта четность не является вызванной центрами. Я видел, что это ошибочно указано на многих разных сайтах и в постах в группе. Однореберная перевернутая четность вызвана решением центров таким образом, что части ребер находятся в нечетной перестановке.
Вот все приемы, которые я использую в этом случае.
Все кубы имеют одинаковую ориентацию, как показано на диаграмме ниже,
Чистая форма
Вот чистая форма алгоритма, который я использую,
r2 B2 U2 l U2 r’ U2 r U2 F2 r F2 l’ B2 r2
А вот влияние на куб этого алгоритма,
Формы Speedsolve
Это самый общий случай применения формы speedsolve,
(Rr)2 B2 U2 (Ll) U2 (Rr) ‘ U2 (Rr) U2 F2 (Rr) F2 (Ll)’ B2 (Rr)2
выполняется как: [(Rr) (Ll)] U2 x U2 (Ll) U2 (Rr)’ U2 (Rr) [( U’) (u d’ D’)] L2 y’ x (Rr) U2 (Rr’) B2 (Rr)2
А вот как этот алг влияет на слой U куба,
С помощью этих двух алгоритмов вы можете немного повлиять на LL,
Если вы используете версию алгоритма проверки четности для скорости решения, LL останется полностью ориентированным, что приведет вас прямо к случаю PLL.
Если вы используете чистую форму алгоритма четности, вы закончите с полностью ориентированным LL.
Чтобы решить четность и закончить ориентированным LL, выполните: R2 B2 R2 (скорость решения алгоритма четности) R2 B2 R2
Чтобы решить четность и закончить ориентированным LL, выполните: L U L’ (форма алгоритма четности для быстрого решения) L U’ L’
Чтобы решить четность и закончить с ориентированным LL, выполните: (r’ l) (скорость решения алгоритма четности) (r l’)
Контроль четности PLL
Контроль четности PLL вызывается во время шага фронтов. При формировании ребер у вас есть только 50-50 шансов создать цикл среди тех ребер, который имеет ту же четность, что и угловая перестановка. Четность перестановки углов и ребер должна быть одинаковой, чтобы куб можно было решить как 3x3x3. Если это не так, вы получите четность PLL.
В этом деле нет особых уловок, только два случая.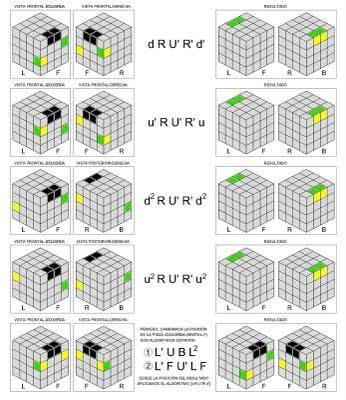
(Uu)2 (Ll)2 U2 l2 U2 (Ll)2 (Uu)2
выполняется как: [(Uu)’]2 [(Ll)’]2 (U’)2 ([(Ll )’]2 L2) (U’)2 [(Ll)’]2 [(Uu)’]2
| . )2 D’ L2 в исполнении: L2 D x [(Uu)’]2 [(Ll)’]2 (U’)2 ([(Ll)’]2 L2) (U’)2 [(Ll)’]2 [(Uu)’ ]2 x’ D’ L2 Этих последних двух случаев можно избежать почти в 100% случаев при тщательном планировании заранее, но если вы все же столкнетесь с одним из них, вы должны знать, как его решить. (Uu)2 (Ll)2 U2 l2 U2 (Ll)2 (Uu)2 F’ U’ F U F R’ F2 U F U F’ U’ F R выполняется как: [(Uu)’]2 [(Ll)’ ]2 (U’)2 ([(Ll)’]2 L2) (U’)2 [(Ll)’]2 [(Uu)’]2 y [(L U’ L) (U)] [(L F ‘ L2) (U)] (L U L’) (U’ L F) (Uu)2 (Ll)2 U2 l2 U2 (Ll)2 (Uu)2 R U’ L U2 R’ U R L’ U’ L U2 R’ U L’ U выполняется как: [(Uu)’ ]2 [(Ll)’]2 (U’)2 ([(Ll)’]2 L2) (U’)2 [(Ll)’]2 [(Uu)’]2 (RU U’) (L U2) (R’ U R) (L’ U’ L) U2 (R’ U L’) (U) Приложение A 3х3. Похожие записи
Об авторе alexxlab |
