Зеркала френеля: Зеркала Френеля.

Зеркала Френеля.

Два
плоских соприкасающихся зеркалаОМ
и ON
располагаются так,
что их отражающие поверхности образуют
угол, близкий к л (рис. 121.1). Соответственно
угол ф на рисунке очень мал. Параллельно
линии пересечения зеркал О
на расстоя­нии г
от нее помещается
прямолинейный источник света S
(напри­мер, узкая светящаяся щель).
Зеркала отбрасывают на экран Э
две цилиндрические
когерентные волны, распространяющиеся
так, как если бы они исходили из мнимых
источников Si
и Si.
Непро­зрачный экран
Э преграждает
свету путь от источника S
к эк­рану Э.

Луч
OQ
представляет собой
отражение луча SO
от зеркала ОМ,
луч ОР
— отражение луча SO
от зеркала ON.
Легко сообразить, что
угол между лучами ОР
и OQ
равен 2ф. Поскольку S
и Si
распо­ложены относительно ОМ
симметрично, длина
отрезка OSi
равна OS,
т. е. г. Аналогичные
рассуждения приводят к тому же резуль­тату
для отрезка OS₂.
Таким образом, расстояние между
источни­ками Si
и S2
равно

Из
рис. 121.1 видно, чтоСледовательно,где ь —
расстояние от линии пересечения зеркал
О до
Ширина интерференционной полосы:

(121.1)

Максимальное число
интерференционных полос, которое можно
наблюдать с по­мощью зеркал Френеля
при данных параметрах схемы:

(121.2)

20.10).

Изготовленные
из одного куска стекла две призмы с
малым преломляющим углом д имеют одну
общую грань (рис. 121.2). Параллельно этой
грани на расстоянии а от нее
рас­полагаетсяпрямолинейный источник
светаS.

Можно
показать, что в случае, когда преломляющий
луч призмы очень мал и углы падения
лучей на грань призмы не очень велики,
все лучи отклоняются призмой на
практически одинаковый угол, равный

(п —
показатель преломления призмы). Угол
падения лучей на бипризму невелик.
Поэтому все лучи отклоняются каждой из
по­ловин бипризмы на одинаковый угол.
В результате образуются две когерентные
цилиндрические волны, исходящие из
мнимых источников Si
и S₂,
лежащих в одной плоскости с S.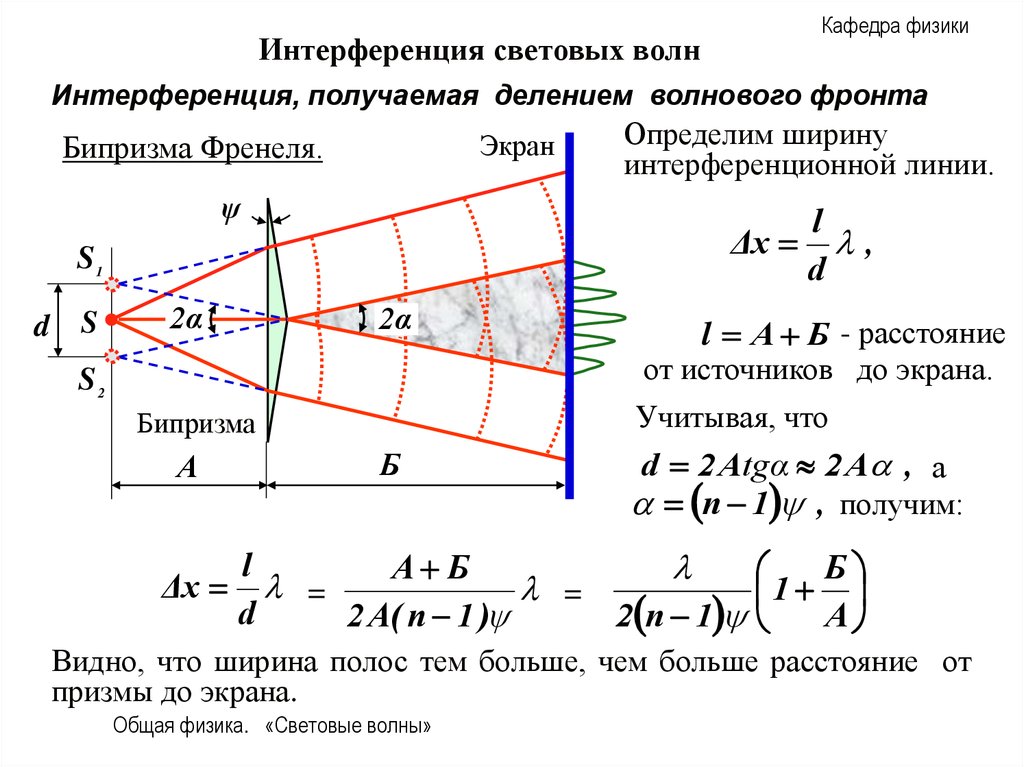
Расстояниемежду источниками равно

Максимальное число
наблюдаемых полос

(121.4) Расстояние
от источников до экрана

Двухлучевая
интерференция

Пусть
световые волны, испускаемые источниками
S₁иS₂,
являются монохроматическими с одинаковой
и постоянной частотойω, а в
рассматриваемой точке наблюденияР(см.рис.1) оба вектораE₁иE₂параллельны
друг другу, тогда их можно считать
скалярными величинами и записать
результирующую напряженность
электрического поля в точкеРв
соответствии с принципом суперпозиции
(1) в следующем виде:Ер = Е1₀
cos
(ωt – kz₁)
+ E2₀cos
(ωt – kz₂)
(9)

Для сложения двух
гармонических функций удобно пользоваться
методом фазовых диаграмм. При этом
напряженность электрического поля
волны представляется как проекция на
некоторую ось00‘ вектора
по величине равного амплитуде волны,
повернутого относительно этой оси на
угол равный фазе волны (см. рис. За).

Рис.3. Фазовые
диаграммы одной волны — (а) и двух — (в),
налагающихся волн.

Если координата
точки наблюдения и положение источника
неизменны, то во время наблюдения
расстояние z постоянно, и фаза волны будет зависеть
только от времени. С течением времени
фаза волны будет расти и векторЕ₀будет вращаться с частотойωотносительно выбранной оси. Проекция
вектора при этом будет изменяться по
гармоническому закону в соответствии
с уравнением:

E(t)
= Eo cos (ωt + φ )
(10)

где φ— начальная
фаза волны, зависящая отz.

При
сложении двух волн, каждая из них
представляется проекцией соответствующего
вектора на выбранную ось, и результирующая
волна равна сумме проекций (см. рис.Зв).
Результат не изменится, если сначала
сложить вектора, а затем взять проекцию.

Так
как для нахождения интенсивности
достаточно знать амплитуду результирующей
волны (см. формулу 2), то после сложения
векторов можно и не искать проекцию
результирующего вектора на ось, а
ограничится найденой амплитудой
результирующей волны (Ер₀)
и определить интенсивность света в
точке наложения.

Из
рис. Зв видно, что амплитуда результирующего
вектора не зависит от фаз налагающихся
волн (фазы волн изменяются с течением
времени, что приводит к синхронному
вращению векторов), а зависит лишь от
разности фаз (∆φ) между налагающимися
волнами (на рисунке разность фаз — это
угол между векторамиЕ1₀иE2₀) и
от амплитуд этих волн.

Применяя
теорему косинусов (см. рис.Зв), можно
записать:

Е_p0²
= Е₁₀²
+ E₂₀²
+ 2E₁₀ ²
E₂₀²cos
∆φ (11)

Так
как интенсивность света (I) пропорциональна
квадрату амплитуды колебаний вектора
напряжённости электрического поля, то
(12)

Последнее слагаемое
называют интерференционным членом. В тех

точках
пространства, для которых cos
∆φ > 0, результирующая интенсивность
(Ip) будет превышать сумму интенсивностейI₁иI₂. В точках, для которыхcos
∆φ < 0,Ipбудет меньшеI₁
+ I₂.

Таким
образом, при наложении когерентных
световых волн происходит перераспределение
светового потока в пространстве, в
результате чего в одних местах возникают
максимумы, а в других — минимумы
интенсивности.

1).Результирующая
интенсивности — I_pпри наложении
двух когерентных волн максимальна

,
если ∆φ = 2πm.(13)

Сравнивая
(7) и (13), можно сказать, что при интерференции
наблюдается максимум интенсивности,если оптическая разность хода двух
интерферирующих волн равна целому числу
длин волн

∆ = тλ(14)

где
m— называется
порядком интерференциии показывает,
сколько длин волн укладывается в
оптической разности хода (m = 0, ±1, ±2,. ..).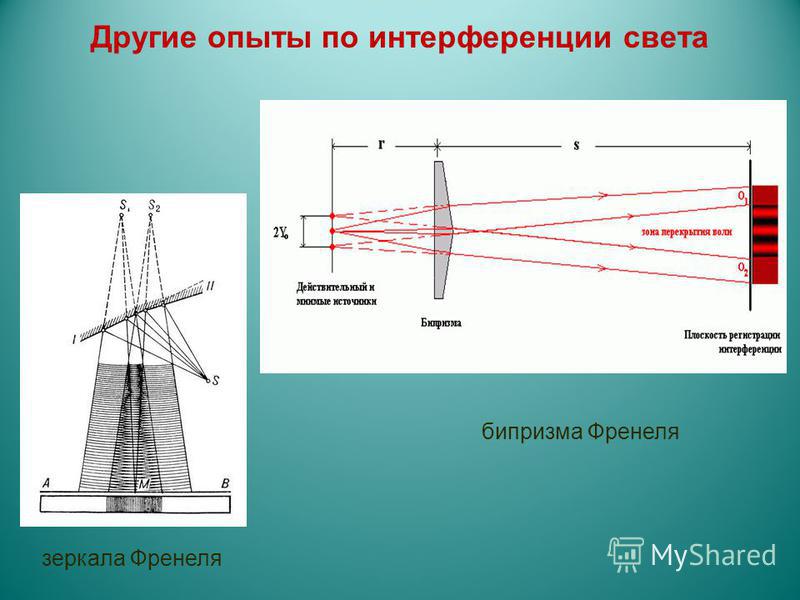

2).Результирующая
интенсивность I — минимальна.

,
если ∆φ = (2m +l)
π, (15)

где — m
= 0, ±1, ±2,…

Т.е.
минимум интенсивностинаблюдается,
если оптическая разность хода равна
нечетному числу полуволн:

∆ = (2m
+1) λ/2. (16)

Для
некогерентных волн ∆φнепрерывно
изменяется, результирующая интенсивностьI_р = 2I₁.

Максимальная
величина оптической разности хода двух
волн, полученных делением одной волны
на части, при которой еще наблюдается
интерференция, называется длиной
когерентности излучения.Длина
когерентности излучения определяется
длиной волны и шириной спектра излучения
и равна

L_K
= λ²/ ∆λ,(I7)

где
∆λ — ширина
спектрального интервала в длинах волн,
в пределах которого интенсивность
излучения отлична от нуля.

Максимальное
значение промежутка времени, при котором
когерентность ещё сохраняется, называется
временем когерентностиизлучения
(t_k)
.

Длина
и время когерентности связаны следующим
соотношением: L
_K
= t
_K
V,
(18) где V
— скорость света.

Основные интерференционные схемы

Для интерференции света необходимым условием является получение когерентных световых пучков. В процессе его выполнения, свое применение находят различные приемы. До того времени, когда во всех приборах для наблюдения интерференции света появились лазеры, когерентные пучки получали с помощью разделения и последующего сведения световых лучей, испускаемым одним и тем же источником. На практике, это может быть осуществимо при помощи экранов и щелей, зеркал и преломляющих тел. Разберем некоторые из таких методов.

Рисунок 1

Метод Юнга и интерференция света

Первое наблюдение явления интерференции световых волн, а также и определение их длин были совершены Т.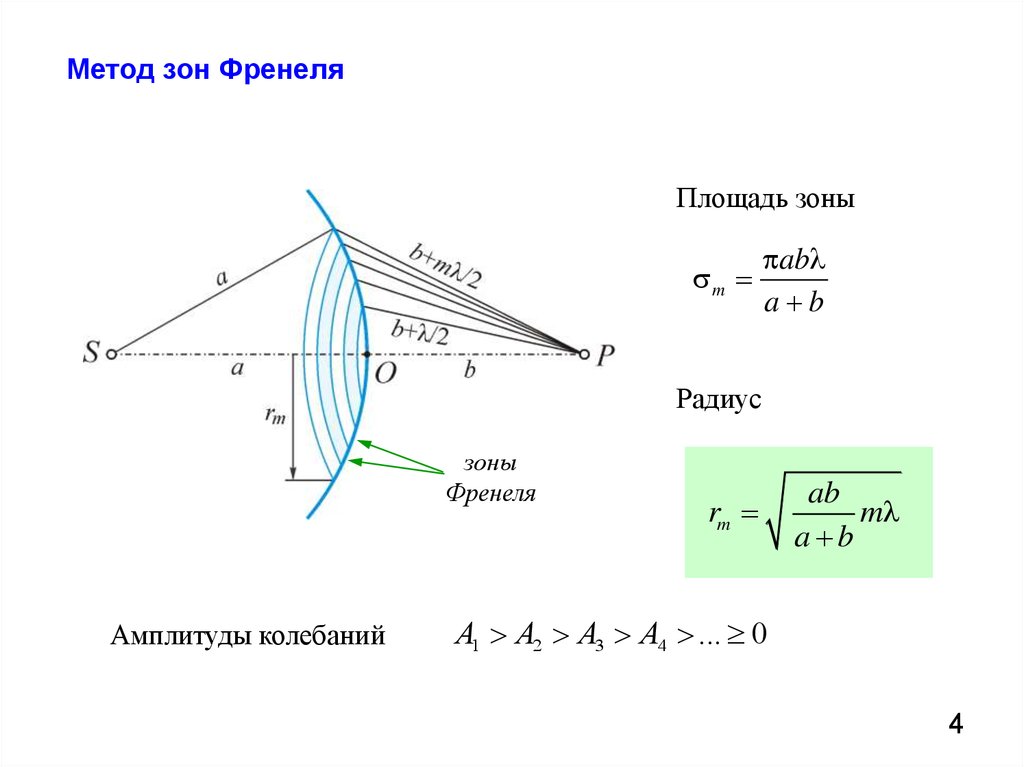 Юнгом. Роль источника света играет ярко освещенная щель S (рисунок 1), из которой световая волна попадает на две параллельные щели S, узкие равноудаленные щели S1 и S2. Исходя из этого, можно сделать вывод, что щели S1 и S2 в данной ситуации являются когерентными источниками. Интерференционная картина (область ВС) наблюдается на экране Э, установленном на определенном расстоянии параллельно S1 и S2.

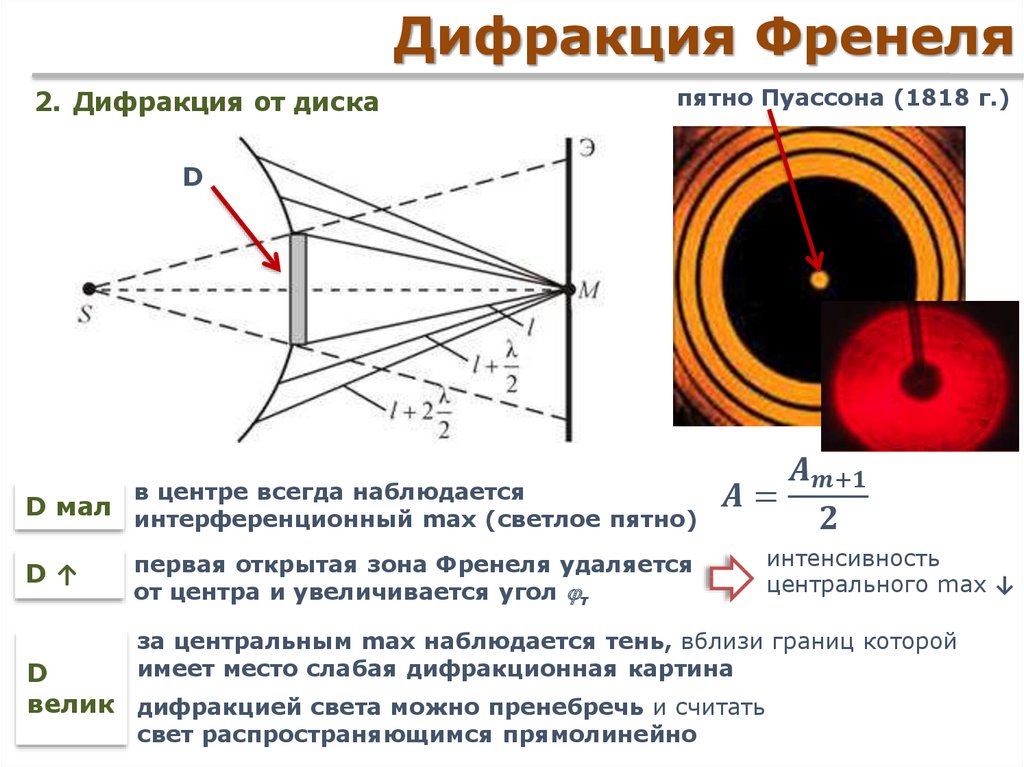
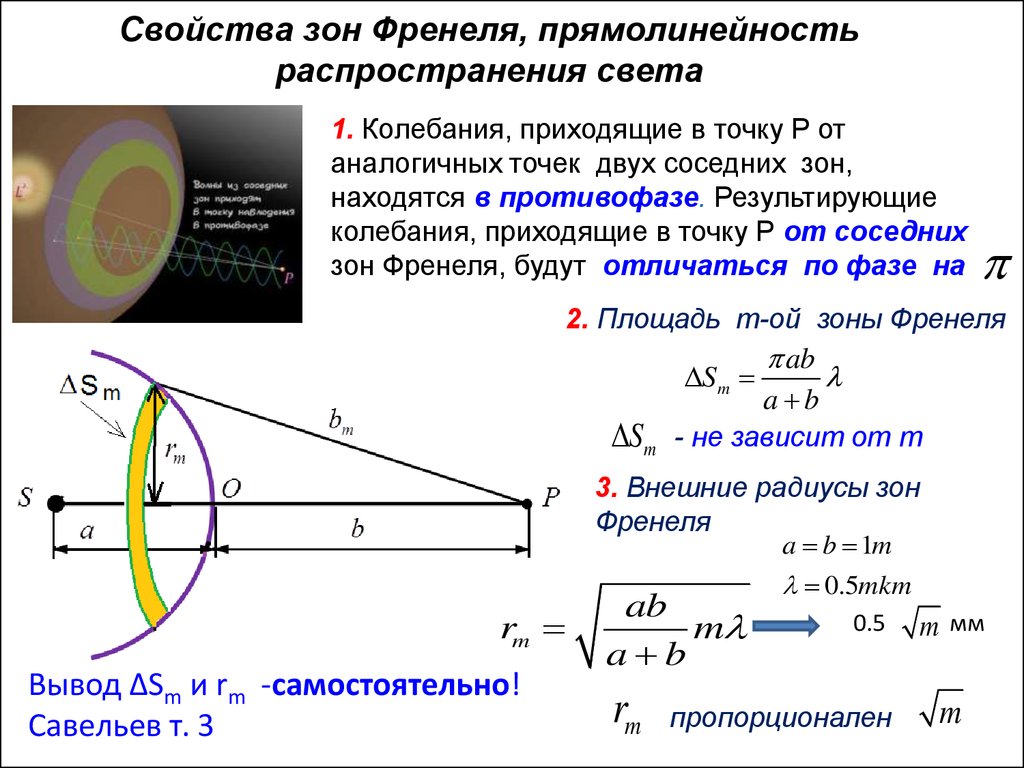
Зеркала Френеля

Пара плоских соприкасающихся зеркал ОМи ON расположены таким образом, что угол между их отражающими поверхностями, крайне близок к нулю (рис. 2). По этой причине угол j на изображении очень мал. Параллельно линии пересечения зеркал О, на некотором расстоянии r от нее, размещается прямолинейный источник света S, такой как, к примеру, узкая светящаяся щель. Зеркала отбрасывают на экран Эдве цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников S1 и S2.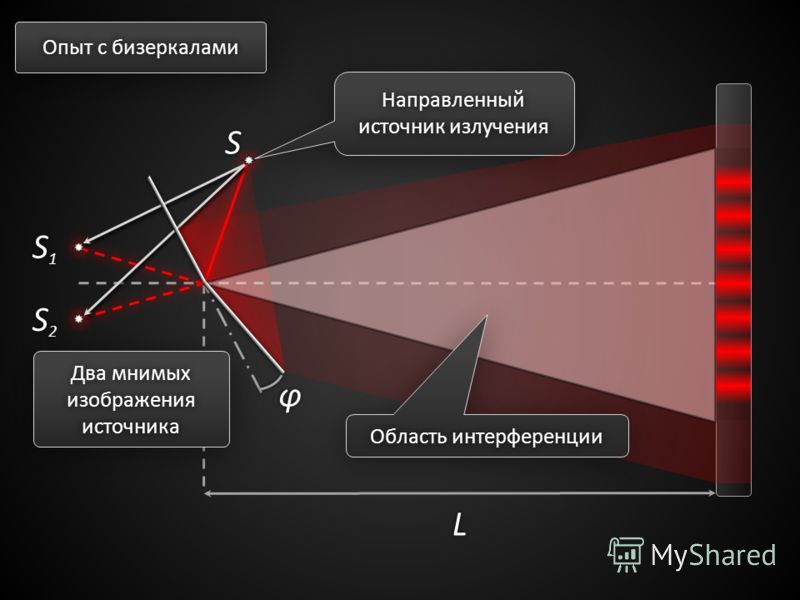 Путь света от источника S к экрану Эпреграждает непрозрачный экран Э1.

Рисунок 2

Луч OQ является отражением луча SO от зеркала ОМ, луч ОР, в свою очередь, представляет собой отражение луча SO от зеркала ON. Несложно понять, что угол между лучами ОР и OQэквивалентен 2j. По той причине, что S1 и S2 располагаются относительно ОМ симметрично, длина отрезка OS1 равняется длине OS, другими словами r. Подобные рассуждения становятся результатом получения того же результата для отрезка OS2. Исходя из вышесказанного, можно заявить, что расстояние между источниками S1 и S2 равно d=2rsin(j)≫2pj.

Бипризма Френеля

Определение 1

Пара изготовленных из одного куска стекла призм с мизерным преломляющим углом q обладают одной общей гранью и называются бипризмой Френеля (рис. 3).

Рисунок 3

Параллельно данной грани на некотором расстоянии a от нее, находится прямолинейный источник света S.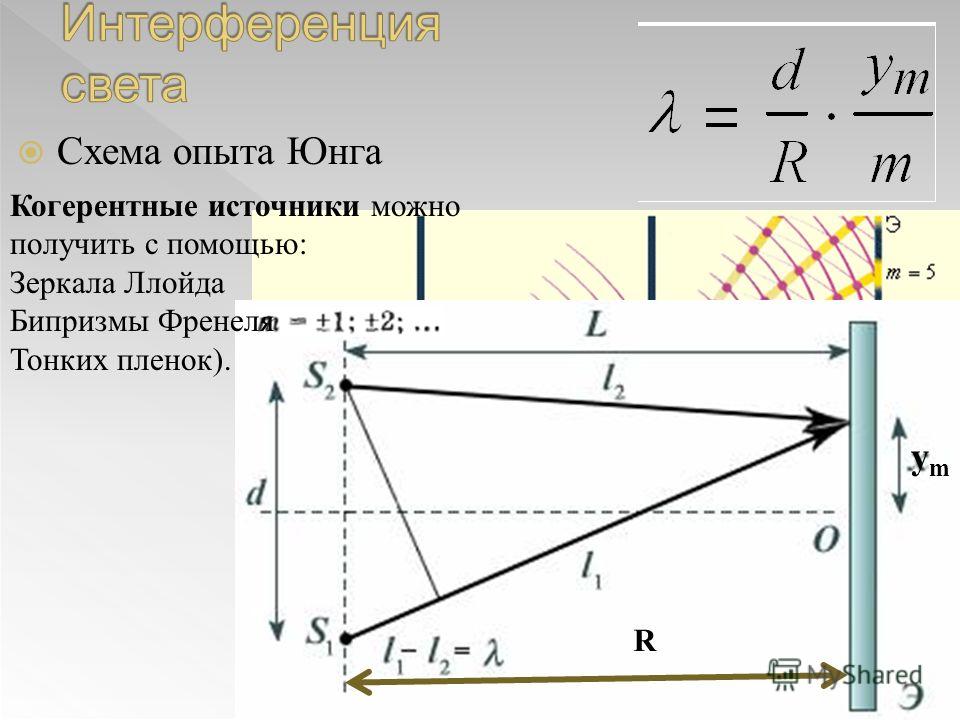 При условии, если преломляющий угол q призмы пренебрежительно мал, а углы падения лучей на грань призмы не сильно велики, то каждый луч отклоняется призмой на почти один и тот же угол, эквивалентный j=(n- l)q, где nпредставляет собой показатель преломления призмы. В случае, когда угол падения лучей на бипризму небольшой, все лучи отклоняются каждой из половин бипризмы на аналогичные углы. Как результат, появляется пара когерентных цилиндрических волн, испускаемых из мнимых источников S1 и S2 и принадлежащих той же плоскости, что и S.

Интерференция проявляется в качестве результата наложения двух расходящихся пучков света, расходящихся от двух когерентных источников, располагающихся на некотором расстоянии lот экрана Э, как это проиллюстрировано на рисунке 1. По данной причине порядок расчета и результат наложения волн будут абсолютно равны.

Определение 2

Область, в которой волны накладываются друг на друга, носит название поля интерференции.

Во всей этой области наблюдается чередование мест с максимальной и минимальной интенсивностью света. Если в поле интерференции поместить экран, то на нем будет проявляться интерференционная картина, выражающаяся в виде чередования светлых и темных полос.

Рисунок 4

Пускай когерентные источники S1 и S2расположены на некотором расстоянии dдруг от друга, а экран Э вместе источниками находится в некой среде с абсолютным показателем преломления n.

Определим оптическую разность хода между когерентными волнами, распространяющимися от источников S1 и S2в приведенную точку M на экране. Точка Mразмещена на расстоянии x от центра интерференционной картины.

∆=L2-L1=r2n-r1n=n(r2-r1),

где L2=r2n и L1=r1 n представляют собой оптические длины пути для первой и второй волн, а r2 и r1 – геометрические длины пути первой и второй волн.

Для случая треугольников S1АМ и S2ВМбудет справедливой следующая запись:

r22=l2+x+d22, r12=l2+x-d22⇒r22-r12=x+d22-x-d22⇒r2-r1r2+r1=2xd.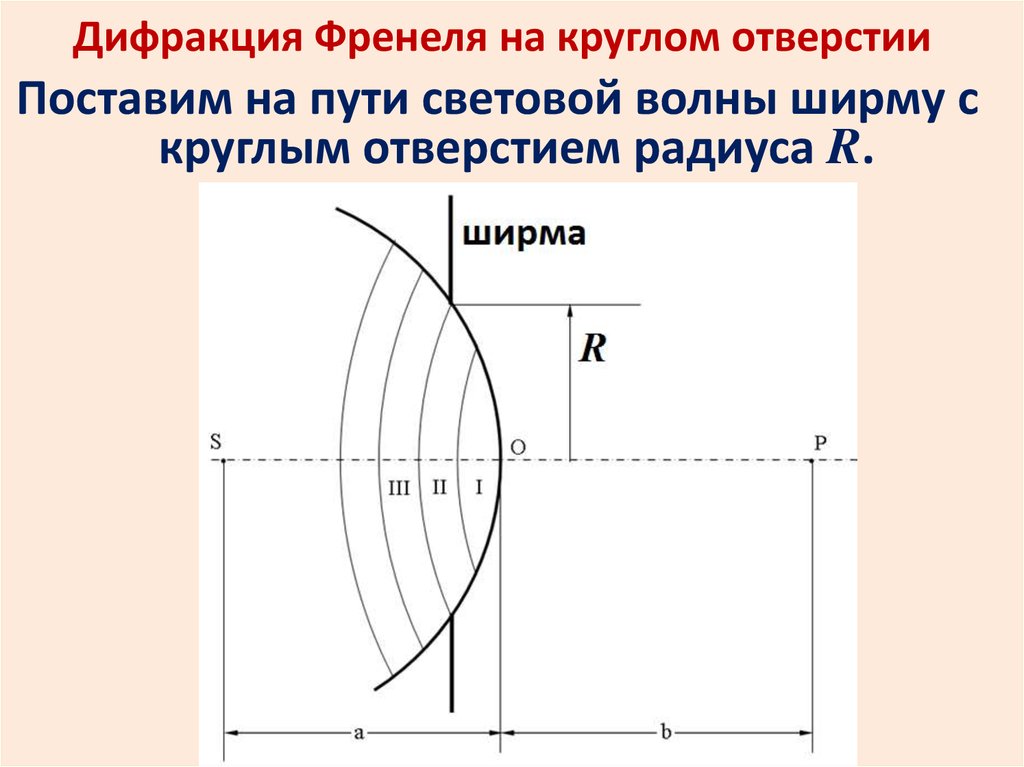

Так как,l≫d , можно заключить, что r2+r1≈2l, учитывая это, выражаем:

r2-r1r2+r1=2xd⇒r2-r12l=2xd⇒r2-r1=xdl.

Оптическая разность ход будет эквивалентна выражению:

∆=n(r2-r1)=nxdl.

Применяя условие интерференционных максимумов для оптической разности хода двух волн в формулу ∆=nr2-r1=nxdl, выведем координаты максимумов, другими словами, положение светлых полос, на экране

nxmaxdl=2mλ2 и xmax=mλlmd, m=0, 1, 2, 3….

Определение 3

В точке xmax=0 размещается максимум, соответствующий нулевой оптической разности хода. Порядок интерференции для такого максимума m=0. Он является центром интерференционной картины.

Подставляя условие интерференционных минимумов для оптической разности хода двух волн в приведенное выражение ∆=nr2-r1=nxdl, определим положение темных полос на экране или же координаты минимумов:

nxmindl=2m+1λ2 и xmin=2m+1λl2nd, m=0, 1, 2, 3…

Определение 4

Расстояние между двумя соседними максимумами (или минимумами), порядок m которых отличается на единицу, определяется как ширина интерференционной полосы.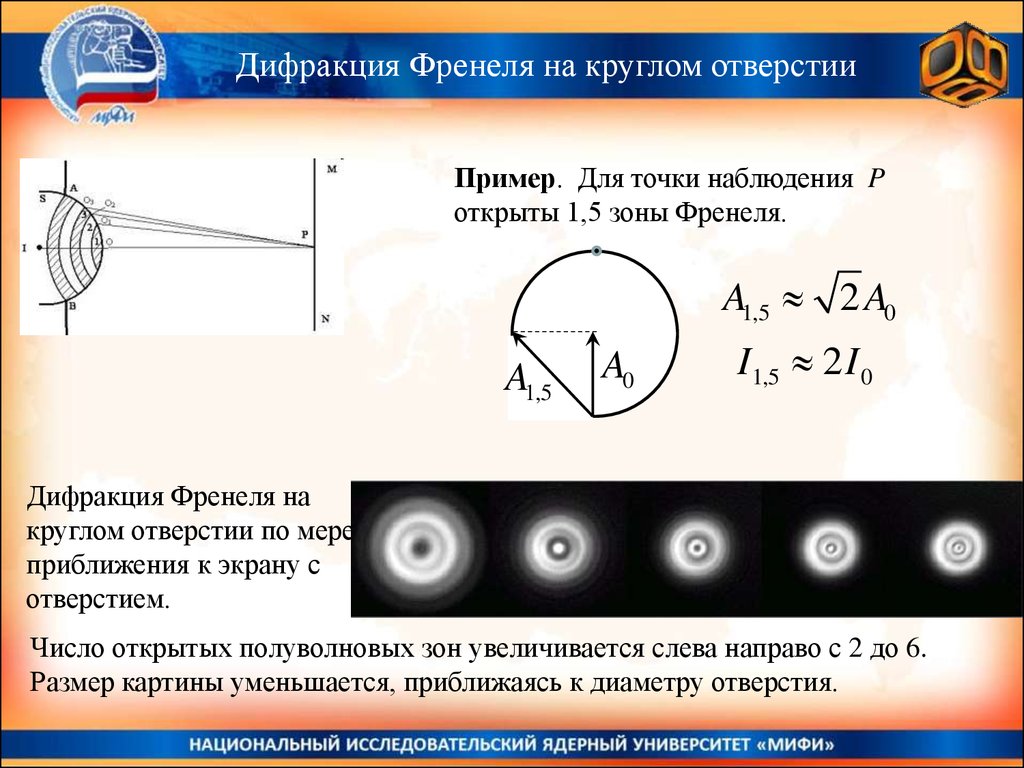

∆x=xm-xm-1=mλlnd-(m-1)λlnd=λlnd.

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Зеркала Френеля Определение и значение

• Лучшие определения
• Викторина
• Примеры

Показывает уровень оценки в зависимости от сложности слова.

Сохрани это слово!

Показывает уровень сложности слова.

существительное во множественном числе Оптика.

Два плоских зеркала, соединенные вместе таким образом, что их можно использовать для изучения интерференционных картин.

ВИКТОРИНА

ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Происхождение зеркал Френеля

Впервые зарегистрировано в 1965–1970 гг.; см. происхождение у Френеля

Слова поблизости Зеркала Френеля

пресноводный барабан, пресноводный жемчуг, френель, бипризма Френеля, линза Френеля, зеркала Френеля, Фресно, фресс, лад, гриф, лад

Dictionary.com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc. 2023

Как использовать зеркала Френеля в предложении

• Это почти отражает буддийский цикл жизни, смерти и возрождения.

  Браконьерская охота на животных ради хорошей кармы|Брендон Хонг|28 декабря 2014|DAILY BEAST

• Ни Иран, ни «Хезболла» не подтвердили эти связи, но риторика и стиль кампании хуситов отражают их обоих.

  Йемен — образец для бедствия|Майкл Шэнк, Кейси Харрити|14 ноября 2014 г.|DAILY BEAST

• В академии есть залы из искусственного мрамора, длинные зеркала и детали, окрашенные в золотой цвет.

  Российская академия золотоискателей|Петр Померанцев|11 ноября 2014 г. |DAILY BEAST

• В романе «Пока мы не смогли» строки о любви великолепны: «Два зеркала лицом к лицу без конца… Да, я считала твои ресницы».

  Посмотрите эту удивительную оду равенству в браке поэта-инаугуратора Ричарда Бланко | Тим Тиман | 21 сентября 2014 г. | DAILY BEAST

• «Многое из того, что происходит в сериале, отражает историю Сиддхартхи, — говорит Яблонски.

  Является ли «Удовлетворение» слишком реальной историей любви о сексе и браке?|Дэвид Маскиотра|19 сентября 2014 г.|DAILY BEAST

• Стеклянные люстры были подвешены к крыше; красивые зеркала перемешались с гравюрами и картинками.

  Журнал о путешествии в Бразилию|Мария Грэм

• Грейс принадлежала к типу Гибсона, высокая, стройная, светловолосая и очень красивая, с явным пристрастием смотреться в зеркала.

  Девушки в седле | Лаура Ли Хоуп

• На практике редко приходится прикасаться к регулировочным винтам самих зеркал.