Получение меандра из синуса: Синус из меандра схема

Синус из меандра схема

Тема в разделе » Бесперебойное аварийное электропитание «, создана пользователем Бигхорн , Искать только в заголовках Сообщения пользователя: Имена участников разделяйте запятой. Новее чем: Искать только в этой теме Искать только в этом разделе Отображать результаты в виде тем. Быстрый поиск. Из инвертора меандр превратить в синусоиду Тема в разделе » Бесперебойное аварийное электропитание «, создана пользователем Бигхорн , Регистрация:

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Из инвертора меандр превратить в синусоиду
• Радиоконструктор — генератор сигналов (меандр, пила, синус) — ICL8038 Function signal generator
• Резонансный фильтр, преобразователь меандр — синус, синусоида. Отзыв, опыт изготовления
• ИБП с правильной (чистой) синусоидой (для котлов и не только)
• Shematic.net
• Генератор сигналов на SigmaDSP, Генератор синуса, меандра, пилы и треугольника
• Резонансный фильтр, преобразователь меандр — синус, синусоида. Отзыв, опыт изготовления
• Shematic.net
• Генератор сигналов из набора: плюсы и минусы

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Архив. Как модифицировать меандр

Из инвертора меандр превратить в синусоиду

Что нового? Если это ваш первый визит, рекомендуем почитать справку по сайту.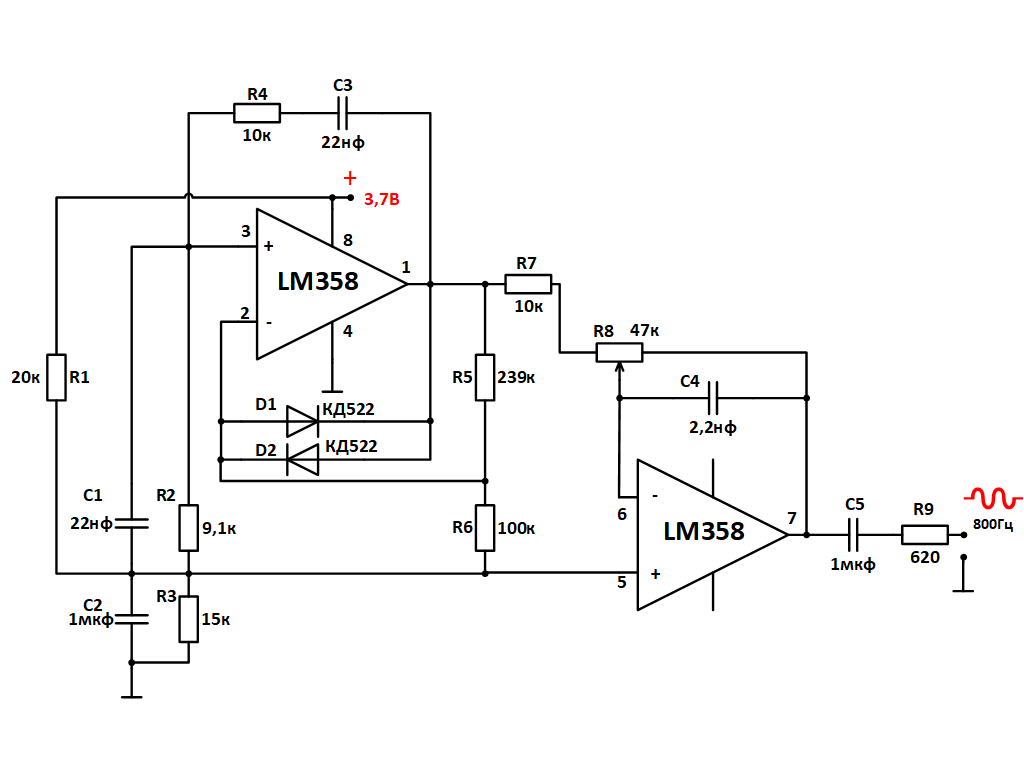 Для того, чтобы начать писать сообщения, Вам необходимо зарегистрироваться. Для просмотра сообщений регистрация не требуется. Забыли пароль? Страница 1 из 2 1 2 К странице: Показано с 1 по 20 из Тема: Меандр из синуса.

Опции темы Версия для печати Отправить по электронной почте… Подписаться на эту тему…. Меандр из синуса. Доброго времени суток, уважаемые форумчане!

Откопал недавно самодельный отцовский генератор ЗЧ, который он сделал ещё в х. Схема на КУН7, синус на выходе чистый, но понадобилось из этого синуса сделать такой же чистый меандр и просто тумблером переключать меандр-синус. Как это лучше реализовать? Может КМОП на выход поставить, а тумблером переключать выход? Схема, судя по всему вот эта, по крайней мере похожа:. Учиться лучше на чужих ошибках, нежели на своих ошибках учить других, но так бывает не часто Скиф Просмотр профиля Сообщения форума Созданные темы.

Re: Меандр из синуса. Борисыч44 Просмотр профиля Сообщения форума Созданные темы. Без лампочки на выходе вообще ничего нет, регулятор там стоит 1к, но это не проблема, т.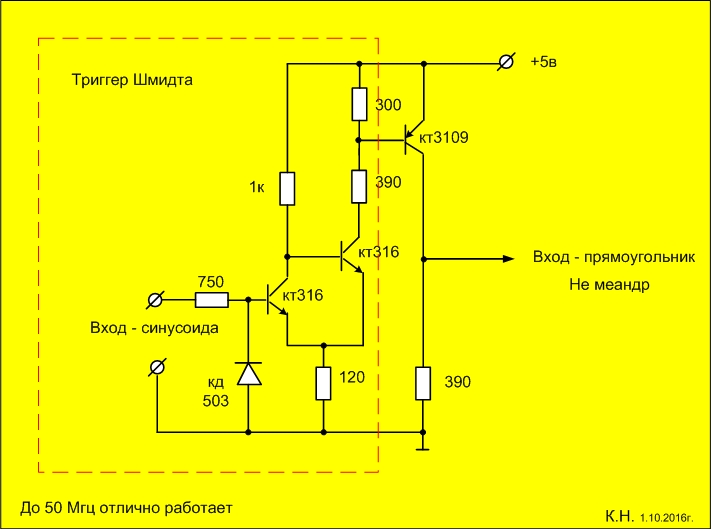 Батя его делал для настройки магнитофонов, этого хватало.

А вот для настройки УМ маловато, хочу поднять вольт до , поэтому выход по любому буду усиливать. У меня есть одна штучка 74ас02, осталась от клок-генератора, пойдёт сюда или поискать что то из отечественных? Сообщение от spiridonoff. Усилить сигнал придётся до кмоп, т. Вообщем то заработало как надо. С выхода гена поставил усилитель на ОУ, тем самым подняв уровень синуса до 3В вместо 0,6В. На выход подключил КЛП Не скажу что меандр получился идеальный, но вполне сойдёт для настройки УНЧ а мне для этого и нужно.

Фронты довольно крутые, можно сказать чистый прямоугольник, а вот звон маааленький всё таки есть на переднем фронте, его практически не видно но он есть. Частично решил проблему введением параллельной RC-цепочки между входом и выходом КЛП12, дальше бороться со звоном не стал, т.

Короче получился вполне сносный меандр, сравнивал с выходом калибратора осцилла, почти то же самое. Спасибо за советы, если интересно могу набросать схемку что получилось, хотя там и ничего особенного нет.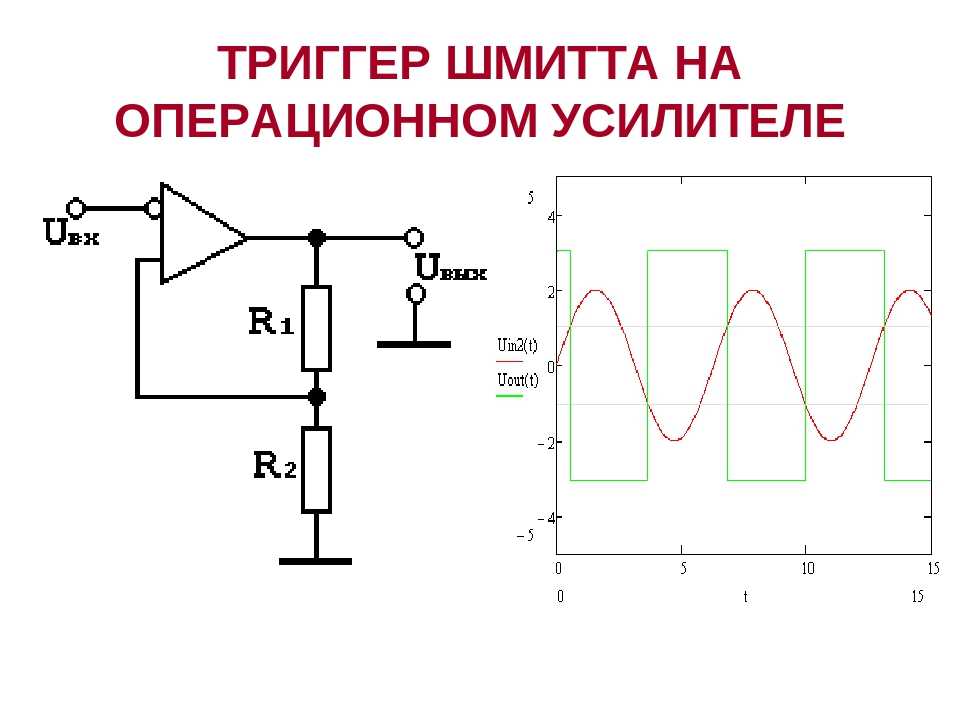

Фронты довольно крутые, можно сказать чистый прямоугольник, а вот звон маааленький всё таки есть на переднем фронте. Может Вы и правы, но питание на ЛП-шку идёт через , куда ж ещё стабильней.

Но так как спаял на макетке, может какая то паразитная связь и образовалась из-за соплей. Попробую завтра поколдовать Ну это понятно, ЛМ-ку может вышибить пусковым током Alex Просмотр профиля Сообщения форума Домашняя страница Созданные темы. Сообщение от Борисыч Воробьев Просмотр профиля Сообщения форума Созданные темы. За все время обсуждения можно было бы давно собрать неплохой функциональный генератор синус, меандр, треугольник. Не слышащий, да увидит! Вот собственно что получилось, никакие пляски с бубном вокруг питания ничего не дали, абсолютно СтОит ли обращать внимание на этот «зубчик»?

Понимаю, если бы я делал генератор с нуля, я бы сделал его по другому, но понадобилась лишь не большая доработка по усилению вых. Значит пойдёт. Сообщение от А. Yours Aye, Ilya. Страница 1 из 2 1 2 К странице:. FAQ, технологии, электронные компоненты и измерения Кабинет А.

Социальные закладки Социальные закладки Digg del. Смайлы Вкл. HTML код Выкл. Текущее время: All rights reserved.

Радиоконструктор — генератор сигналов (меандр, пила, синус) — ICL8038 Function signal generator

Поиск новых сообщений в разделах Все новые сообщения Компьютерный форум Электроника и самоделки Софт и программы Общетематический. Простой генератор синуса и меандра. А зачем два переменных резистора? Я бы взглянул на спектрограмму. А можно еще увидеть осциллограмму на самой низкой частое? Можно , но только завтра , сегодня уж устал , недавно только с работы приехал. Ads Яндекс.

Схема на КУН7, синус на выходе чистый, но понадобилось из этого синуса сделать такой же чистый меандр и просто тумблером.

Резонансный фильтр, преобразователь меандр — синус, синусоида. Отзыв, опыт изготовления

Технический портал радиолюбителей России. Фотогалерея Обзоры Правила Расширенный поиск. Уважаемые посетители! RU существует исключительно за счет показа рекламы. Мы будем благодарны, если Вы не будете блокировать рекламу на нашем Форуме. Просим внести cqham. Страница 1 из 4 1 2 3 4 Последняя К странице: Показано с 1 по 10 из

ИБП с правильной (чистой) синусоидой (для котлов и не только)

Генератор сигналов был в лаборатории нашего института — это такой большой ящик с десятком ручек регулировки. Он был ламповый и грелся минуты три до выхода на нормальный режим работы. Может ли маленькая платка за 7 долларов выполнять основные его функции? Прямоугольный сигнал: Амплитуда без нагрузки: 8 Вольт при питании 9 Вольт.

Авторизация Зарегистрироваться Логин или эл.

Shematic.net

By Спиридонов , March 23, in Измерительная техника. Есть самодельный генератор синуса ЗЧ на кун7, как можно на его основе получить на выходе меандр. Суть в том, чтобы из синуса при общей настройке частоты на выходе получить меандр, то есть чтобы можно было переключать выход генератора на синус или меандр, а не городить отдельный генератор меандра. Так как частотная шкала откалибрована под синус, и сделана очень удобно, не хотелось бы это трогать. Пробовал КМОП, получается не меандр, а импульсы с определённой скважностью.

Генератор сигналов на SigmaDSP, Генератор синуса, меандра, пилы и треугольника

Но больше всего заказов поступает на ИБП с правильной синусоидой — их покупают для котлов отопления, серверов, насосов. Что это, почему именно они, чем такие бесперебойники отличаются от других видов? Мы постараемся ответить в этой статье на наиболее частые вопросы наших покупателей. В представлении многих ИБП — это устройство, которое при отключении питания некоторое время поддерживает работу подключенной к нему техники. Все верно, но не все так просто. А все потому, что есть такой значимый параметр, как форма выходного сигнала. Вот здесь начинается интересное. Если правильная синусоида может еще называться чистой, в крайнем случае — немоделированной, или «синусоидальная форма», то в обозначении формы сигнала, не соответствующей синусоиде, фантазия производителей не знает границ.

Резонансный фильтр, преобразователь меандр — синус, синусоида.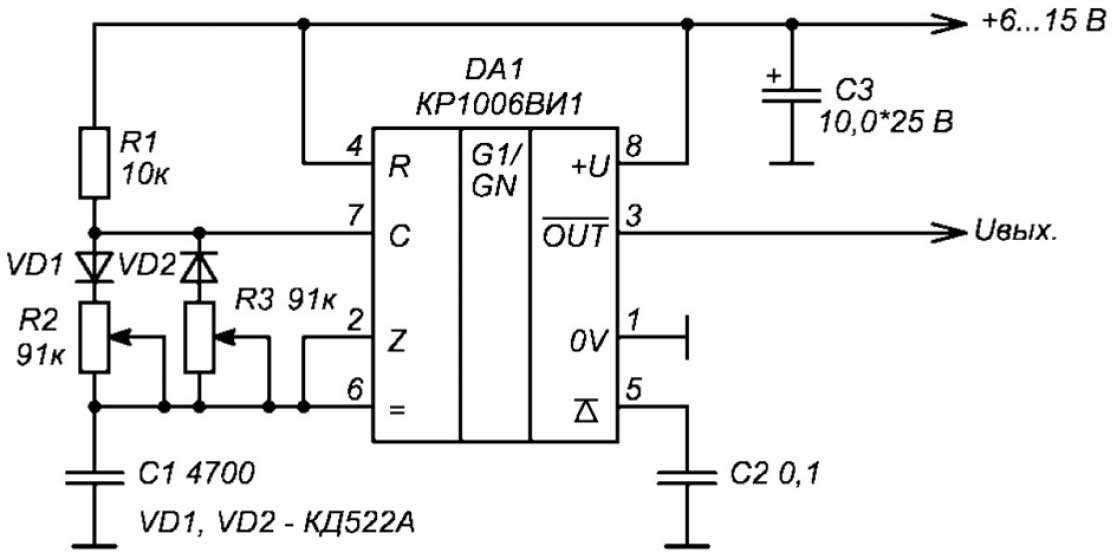 Отзыв.. Схема инвертора с чистой синусоидой.

Резонансный фильтр, преобразователь меандр — синус, синусоида. Отзыв, опыт изготовления

Получение выходного биполярного сигнала с логики Добрый день. Подскажите пожалуйста, где в мультисиме найти инвенторы с отрицательным логическим Генерация синуса, трапеции, меандра и треугольного сигнала WAV Здравствуйте, подскажите пожалуйста. Нашёл пример для записи в WAV синусоидального сигнала.

Shematic.net

Полезные советы. Почему нельзя использовать компьютерный UPS для питания котла Возможно ли отфильтровать модифицированный синус? Резонансный фильтр, преобразователь меандр — синус, синусоида. ИБП с правильной чистой синусоидой для котлов отопления, серверов.

Запомнить меня.

Генератор сигналов из набора: плюсы и минусы

Правила форума. RU :: Правила :: Голосовой чат :: eHam. Страница 1 из 2 1 2 Последняя К странице: Показано с 1 по 15 из Тема: Как Из Синусоиды Добавить тему форума в del. Закладках Разместить в Ссылки Mail.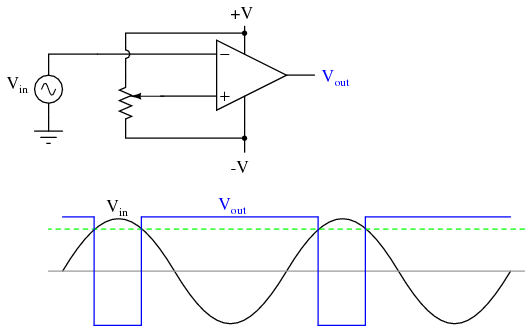

Запросить склады. Перейти к новому. Из меандра синус.

Фильтр Отто или синус из меандра

Немного заинтересовавшись синусом набрел на интересный материал Володина Валентина из Одессы. Это фильтр Отто. С практической стороны, если простыми словами преобразуем синус из меандра

Зачастую для питания бытовых электроприборов, в отсутствии напряжения сети,
используются различные преобразователи постоянного напряжения в переменное,
формирующие переменное напряжение прямоугольной формы.
Практика показала, что большинство обычных бытовых электроприборов вполне прилично работает от такого напряжения.

Однако существуют электроприборы, которые напрочь не хотят работать от такого
напряжения – это однофазные конденсаторные асинхронные двигатели. Такими
двигателями, например, комплектуются циркуляционные насосы различных систем отопления импортного и отечественного производства. Разумеется, в таком двигателе, при питании его прямоугольным напряжением, содержащим большое количество гармоник, не может возникнуть равномерно вращающееся магнитное поле и двигатель если и вращается, то крайне неравномерно. Выход может быть в питании двигателя синусоидальным напряжением.

Как уже говорилось, сформировать синусоидальное напряжение из прямоугольного можно, используя различные фильтры выделяющие основную гармонику. Наилучшим образом для такой цели подходит, так называемый, фильтр Отто (рис.1), передающий в нагрузку первую гармонику практически без ослабления и максимально ослабляющий высшие гармоники.

Из рис.1 видно, что фильтр состоит из последовательного и параллельного
колебательных LC-контуров, каждый из которых настроен на первую гармонику входного напряжения. Здесь сразу следует оговориться, что фильтров, одинаково хорошо работающих с любым типом нагрузки, не существует. Наилучшим образом фильтр работает только с той нагрузкой, на которую он рассчитан.

Рассчитаем параметры фильтра для случая его использования совместно с асинхронным двигателем. Параметры двигателя, присутствовавшие на его шильдике, отображены в таблице:

Индуктивная составляющая Lд сопротивления двигателя может быть использована в качестве элемента фильтра (рис.2).

Здесь сопротивление RL характеризует активные потери в дросселе, а Rд — активные потери в двигателе. Активные потери, возникающие в конденсаторах C1 и C2 в расчёт не берутся. Исходя из cosϕ, сдвиг между напряжением и током двигателя, в номинальном режиме, будет ϕ=53° , а sinϕ=0.8.
Активная составляющая, потребляемого двигателем тока:
IR=P/U=75/220=0.341 А
Реактивная составляющая, потребляемого двигателем тока:
IL=IR⋅(sinϕ/cosϕ)=0.341⋅0.8/0.6=0.454 А
Откуда RД=U/IR=220/0.341=645 Ом
Индуктивное сопротивление индуктивности Lд:
XLд=U/IL=220/0.454=484 Ом
Собственно индуктивность:
Lд=XLд/ω=484/314=1.51 Гн
Где ω=2⋅π⋅F=2⋅3.14⋅50=314 рад/сек

Ориентировочно зная величину индуктивности Lд, можно выбрать величину
конденсатора C2, руководствуясь необходимостью получения резонанса токов на частоте 50Гц.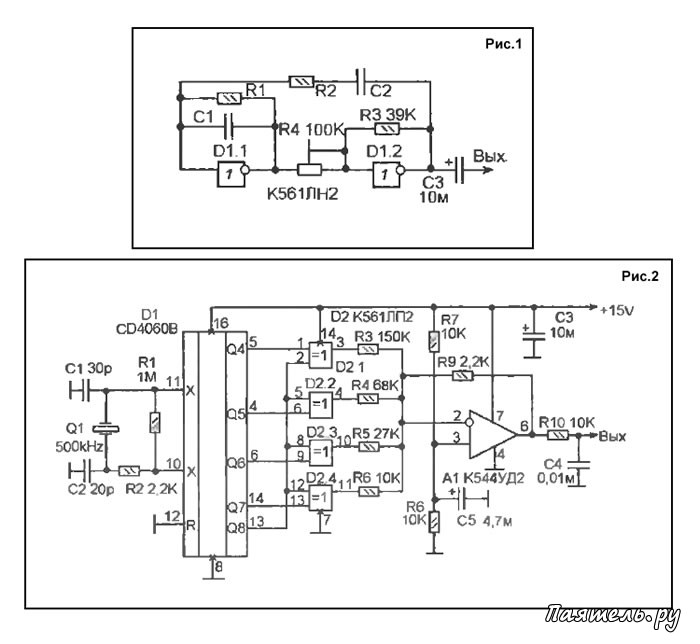 2⋅1.51)=6.58 мкФ
При резонансе в контуре LДС2 реактивная составляющая тока двигателя
скомпенсирована током конденсатора С2 и поэтому данный контур потребляет только активный ток. Зная активный ток, потребляемый двигателем из сети, можно
регламентировать этот параметр для индуктивности L1, в качестве которой, например, можно использовать дроссель от светильника дневного света с лампой мощностью 80 Вт.
На дросселе имеются следующие исходные данные, характеризующие параметры
светильника:

Температурный режим дросселя будет в норме, так как его рабочий ток, приведённый в таблице, превышает активный потребляемый ток двигателя.
Для cosϕ=0.5 следует, что ϕ=60°, а sinϕ=0.866.
Рассчитаем полную мощность, потребляемую светильником из сети:
S=U⋅I=220⋅0.84=184.8 ВА
Активная мощность, потребляемая из сети:
P=S⋅cosϕ=184.8⋅0.5=92.4 Вт (из которых 80 Вт рассеивается в лампе и 12.4 Вт
рассеиваются на внутреннем сопротивлении дросселя RL)
Сопротивление активных потерь:
R=P/I^2=92. 2, где n – номер гармоники.
При найденных выше значениях L1 и LД третья гармоника (частота 150 Гц) будет
подавлена в 3.4 раза, пятая (250 Гц) в 11, седьмая (350 Гц) – в 22.5 и девятая (450 Гц) – 37.5 раз. Чётные гармоники отсутствуют.
На данном этапе неплохо было бы убедиться, что частоты ν1⋅F и ν2⋅F не совпадают ни с одной из гармоник присутствующих на входе фильтра.
Эти частоты можно определить из формулы [1]:
В нашем случае ν1⋅F=33.3 Гц, а ν2⋅F=75 Гц, что не совпадает ни с одной
из гармоник. В противном случае нужно изменить величину индуктивности L1 и произвести перерасчёт.
Теперь следует оговориться о выборе амплитуды входного прямоугольного
напряжения, обеспечивающей получение необходимой амплитуды напряжения первой гармоники на выходе фильтра. Предварительно следует учесть падение напряжения на внутреннем сопротивлении RL дросселя L1.
URL=IR⋅RL=0.341⋅20.46=7 В
Следовательно нам необходимо действующее напряжение первой гармоники
U1г=220+7=227 В.

Для формы напряжения, изображённой на рис.3, амплитуда напряжения на выходной обмотке преобразователя равна:
Uтр=U1г⋅1.11=227⋅1.11=252 В.
Для других форм входного напряжения гармонический состав можно оценить пользуясь рекомендациями.
Детали:
Конденсаторы С1 и С2 составлены из параллельно соединённых конденсаторов КБГМН, МБГЧ, МБГП, МБМ. Рабочее напряжение конденсатора С1 не менее 400 В, а конденсатора С2 не менее рассчитанного.
Настройка:
Любой фильтр требует последующей настройки, т.к. при расчёте мы получаем ориентировочные значения номиналов компонентов. Предлагаю возможную методику настройки. Последовательную и параллельную ветви фильтра, для простоты, лучше настраивать независимо. При настройке можно использовать напряжение сети, разумеется с соблюдением необходимых мер предосторожности. Сначала можно настроить последовательную цепь, нагрузив её на лампочку накаливания мощностью 75 Вт, как это изображено на рис.4.

Добиться минимальных показаний вольтметра переменного
тока, варьируя ёмкость конденсатора С1. Варьировать ёмкость конденсатора можно путём подключения или отключения мелких конденсаторов параллельно основному конденсатору, номинал которого выбирается несколько ниже рассчитанного.
Потом настраиваем параллельную цепь, как это изображено на рис.5.

При настройке двигатель должен работать на холостом ходу, иначе резонансная
характеристика контура будет притуплена, что затруднит настройку. Добиться минимальных показаний вольтметра переменного тока, варьируя ёмкость конденсатора С2. После этого фильтр считается настроенным и можно приступать к его эксплуатации.

Рекомендуемая литература:
1. Ф. Чаки и др.. Силовая электроника. Энергоиздат. Москва 1982г., стр.208-216.
2. Л. А. Бессонов. Теоретические основы электротехники. Высшая школа. Москва
1973г., стр. 228.

За информацию спасибо valvolodib.narod.ru

30keir~1.htm Аппроксимация меандров с помощью синусоидальных кривых

30keir~1.htm Аппроксимация меандров с помощью синусоидальных кривых

Машина обратного пути — http://web. archive.org/web/19991006020149/http://www.woodrow.org:80/teachers/mi/1993/30keir.html

Abstract: Меандр — это кривая, которая возникает естественным образом, когда извилистый объект, такой как река, совершает наименьшую работу при повороте. Хотя его точное представление требует решения эллиптического интеграла, было обнаружено, что построенная по синусоиде кривая служит хорошим приближением. В этой статье будут предложены некоторые действия для изучающих тригонометрию, чтобы получить представление о таких приближениях.

Класс прикладных задач, часто встречающихся в текстах по алгебре, включает вычисление расстояний, времени и скоростей движения объектов по «прямой» реке. Однако реки в природе проявляют такую ​​прямолинейность только на коротких участках; более реалистично, они пересекаются чрезвычайно изогнутыми узорами. Такие кривые называются меандрами, и они развиваются из основной структуры, которая требует от них наименьшего объема работы при повороте. Такое изгибание можно наблюдать и в движении змей, в изгибе пружинной стали и в стабилизирующей конфигурации цепи, возмущенной между неподвижными концами. Математический анализ такой кривизны включает в себя поиск наиболее вероятного пути «случайного блуждания» фиксированной длины и требует решения эллиптического интеграла, что, безусловно, выходит за рамки математики средней школы. Однако, к счастью, извилистую форму можно точно аппроксимировать с помощью синусоидальной кривой, и исследование этого обеспечивает хорошее занятие для изучающих тригонометрию.

Прежде чем мы сможем начать наше исследование, нам нужно установить следующие определения:

среднее направление вниз по долине:

Линия, имитирующая общее направление течения реки. Его можно аппроксимировать, разделив график пополам посередине между верхней и нижней точками амплитуды кривой.

расстояние по каналу:

Длина кривой, измеренная от начальной до конечной точки.

угловое направление канала:

Мера угла касательной к кривой по отношению к среднему направлению вниз по долине.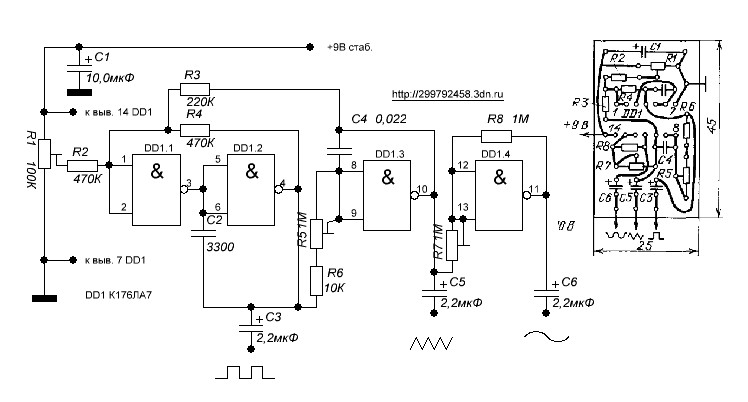 Измерьте его в градусах, необходимых для поворота линии, которая начинается параллельно средней линии направления вниз по долине и заканчивается параллельно касательной в направлении потока канала. Если вращение происходит по часовой стрелке (или вправо), считайте угол отрицательным. Если вращение против часовой стрелки (или влево), считайте угол положительным.

График зависимости между угловым направлением канала (по оси Y) и расстоянием вдоль канала (по оси X) представляет собой приблизительно синусоидальную функцию. Таким образом, по графику меандра можно создать соответствующую синусоидальную функцию, которая его генерирует, с помощью уравнения, а по синусоиде можно создать соответствующий меандр. Мы сделаем пример, чтобы продемонстрировать нашу концепцию измерения углового направления канала, а затем оставим студенту выполнить три упражнения.

Пример:

Иллюстрация 1

Иллюстрация 2

Упражнение 1:

Создайте синусоидальную функцию, график которой соответствует графику зависимости углового направления от расстояния вдоль канала для этого меандра.

Упражнение 2:

Нарисуйте меандр, созданный y = 110 sin 20(x-7), для 0 < x < 30

Упражнение 3:

Попробуйте создать свой собственный меандр. Хорошим устройством для использования является ювелирная цепочка, например, носимая на шее. Поместите цепочку на лист миллиметровой бумаги поверх блокнота или любого другого объекта, который можно «раскачивать». Попросите друга держать концы цепочки, закрепленные на миллиметровой бумаге, а вы осторожно постукивайте по блокноту снизу, пока цепь не стабилизируется в извилистую конфигурацию. Проследите часть кривой, которая больше всего похожа на другие извилистые кривые, которые вы видели. Проведите измерения и посмотрите, насколько точно синусоидальная кривая соответствует данным.

Вопросы для размышления:

Подумайте о том, как параметры периода, фазового сдвига и амплитуды влияют на кривизну меандра. Каким будет визуальный вид меандра, образованного синусоидой малой амплитуды, скажем, 45? ^{Какой будет характеристикой меандра, образованного синусоидой амплитудой 180? Чем бы отличались два меандра, если бы их порождающие синусоиды имели одинаковую амплитуду, но разные периоды? Где вы должны начать измерение длины канала, чтобы получить синусоиду с нулевым фазовым сдвигом?}

Подробный анализ математики меандров и различные графические иллюстрации см.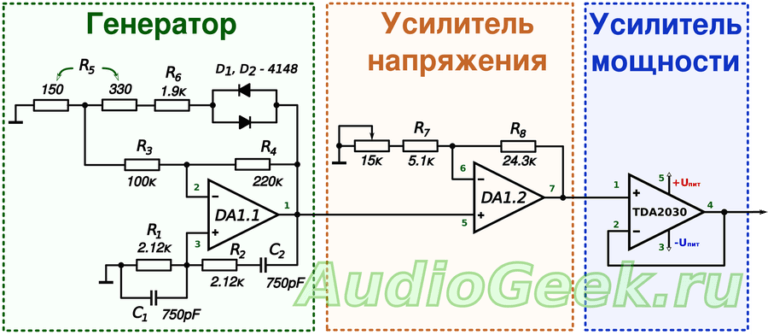 в статье «Меандры рек» Луны Леопольд и В.Б. Лангхейм, Scientific American, , июнь 1966 г.

Извилистые реки – Записная книжка туриста

Река Шенандоа (южная развилка) извивается на север вдоль долины Шенандоа Река Шенандоа, когда они проходят по обе стороны горы Массанаттен. Они извиваются, слово, которое происходит от змеевидного течения рек; река Мендерес в западной части Малой Азии является этимологическим корнем, вошедшим в пословицу из-за ее извилистого течения (в Древней Греции, на исходном языке, она называлась Майандрос). Ярко выраженная и универсальная извилистость извилистых рек уже много лет является предметом научного любопытства естествоиспытателей, геологов и потамологов (специалистов по рекам).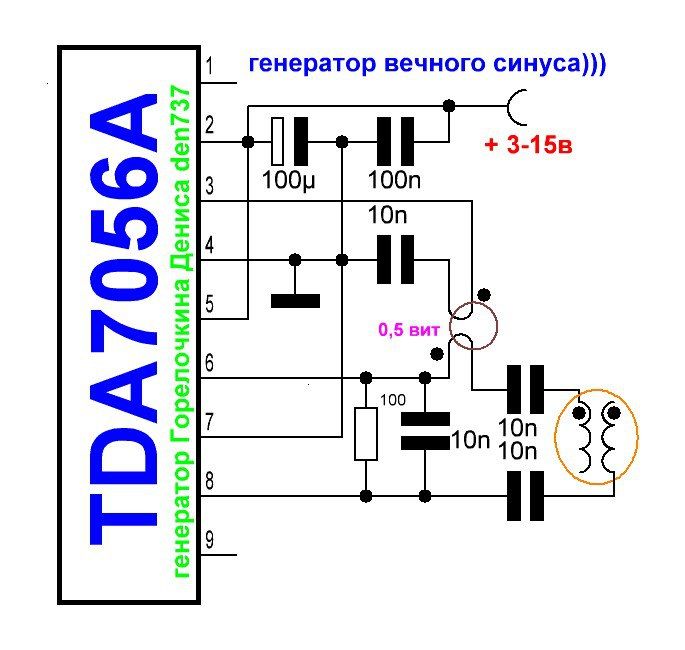 Это привело к серьезным исследованиям с сопутствующим выдвижением гипотез относительно научного объяснения этого явления. Хотя существуют теории причинно-следственной связи, общепринятой доктрины нет.
Фундаментальная физика речного течения пешеходная; вода бежит вниз. Распространение этого принципа на блуждающий путь также кажется довольно очевидным. Местные неровности в русле реки, такие как большие камни, поваленные деревья и пестрый прибрежный осадочный субстрат, могли бы отклонить неумолимую траекторию движения воды вниз. Как только поток отклоняется от препятствия, он усложняется, и в игру вступают капризы и сложности потока жидкости. Но прежде чем это можно будет адекватно решить, необходимо ввести некоторые лексические термины и термины измерений.

Какова природа меандра? Он состоит из трех частей: внешней стороны речной излучины, которая называется вогнутой частью, внутренней стороны речной излучины или выпуклой части и прямой области между последовательными изгибами, которая называется точкой перегиба, потому что она отмечает точка, в которой кривизна изменяется или изгибается из одного направления в другое. Участок реки имеет длину, которая считается расстоянием, которое река проходит над землей, а не расстоянием между двумя точками. Он также имеет ширину и глубину. Поскольку извилистая река имеет чередующиеся изгибы, она подобна волне и, следовательно, имеет амплитуду, длину волны и радиус кривизны. Амплитуда — это расстояние по земле, на которое изгиб реки уходит от общего нисходящего пути реки. Длина волны — это расстояние вдоль земли между последовательными изгибами в одном направлении. Радиус кривизны подобен радиусу окружности; для изгиба реки это радиус дуги, образуемой изгибом.

Возвращаясь теперь к формированию речных излучин; когда встретится препятствие нисходящему течению воды, река будет обтекать его; не симметрично, а в пользу одной стороны. Вода, которая идет по более длинному маршруту, должна двигаться быстрее. Это тот же принцип, который создает подъемную силу в аэродинамическом профиле: верхняя поверхность изогнута, поэтому воздух должен двигаться быстрее, создавая перепад давления.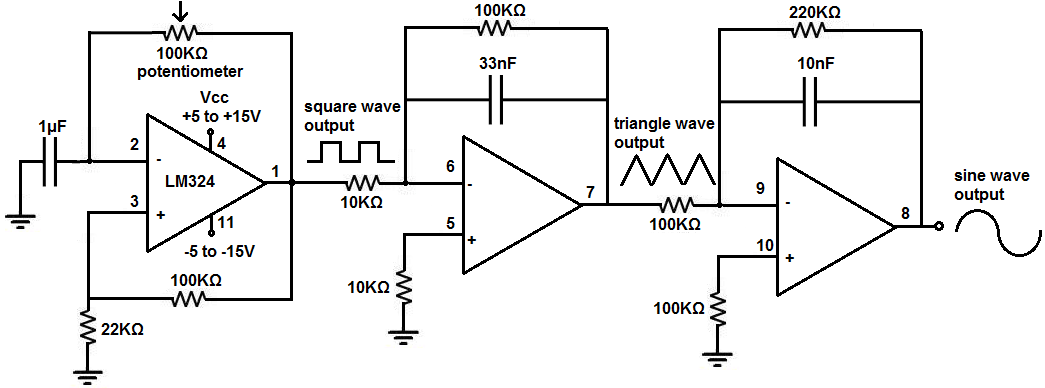 Более быстрый поток вызовет большую эрозию на той стороне препятствия, и в конечном итоге будет сформирован вогнутый берег. Ил, удаленный эрозией, будет перенесен вниз по течению, где он осядет в районе, где поток ослаб, в конечном итоге сформировав бар. По мере продолжения этого процесса вогнутые берега становятся более размытыми, и наносы откладываются по берегам реки, как правило, на выпуклом изгибе следующего изгиба. Таким образом, течение реки является самым быстрым и обтекает берег вогнутой стороной, а в точке заражения переходит на другой берег. Поскольку линии течения реки не совпадают с формой берегов, ей дается специальное название — тальвег, линия самого быстрого течения реки. Это из древнегерманского thal означает «долина» и weg означает «путь»; это также означает линию наибольшего уклона в долине, по которой обычно следует река.

Не меньшее интеллектуальное светило, чем Альберт Эйнштейн, размышляло о происхождении и механизме меандра. Применяя к этой проблеме свои отмеченные «мысленные эксперименты», он сравнил реку с чашкой чая, а листья на дне чашки — с отложениями в реке.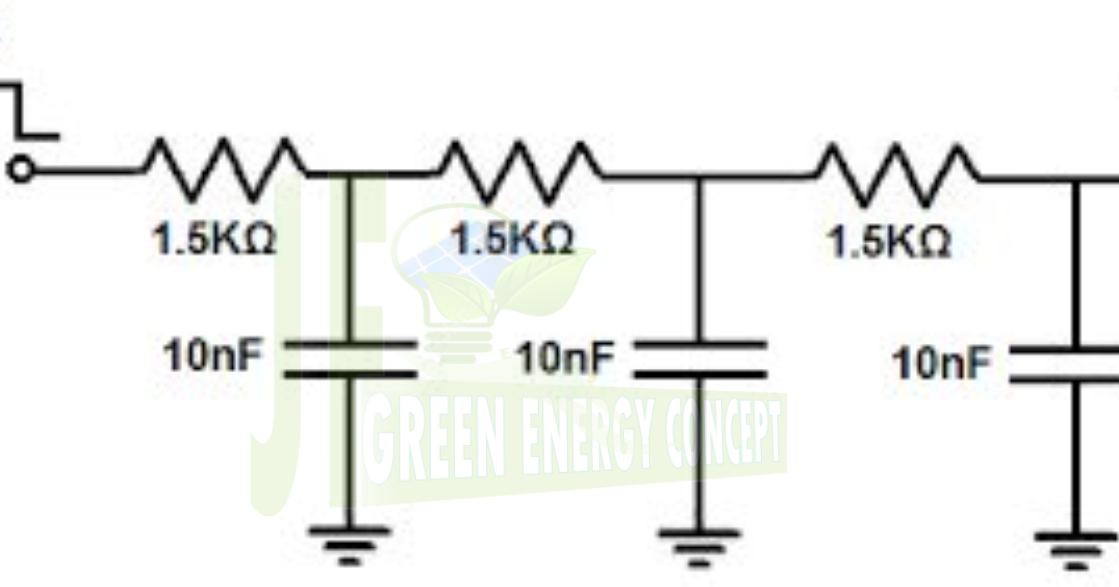 Когда чай перемешивают, листья собираются в центре дна чашки. Объяснение кроется в основах физики. При вращении жидкости создается центробежная сила (сила та, которую вы чувствуете, когда идете за угол). Если бы вся жидкость двигалась с одинаковой скоростью, эффекта бы не было. Однако трение, вызванное стенками и дном чашки, уменьшает вращательное движение и, следовательно, центробежную силу, которая теперь будет меньше у дна. Это создает исходящий поток вверху, который идет наружу, пока не ударится о стену, поток распространяется вниз, чтобы вернуться на дно чашки, где сила меньше. В реке течение реки вниз по течению приводит к спиральному потоку, центробежная сила наверху выталкивает воду наружу и вниз, отталкивая отложения вниз по течению. Эйнштейн далее постулировал, что максимальная эрозия будет происходить ниже по течению от точки перегиба, так что меандр с течением времени будет мигрировать вниз по реке, что является отмеченным и наблюдаемым явлением.

Из приведенного выше объяснения можно сделать вывод, что меандры образуются, когда река течет по пологому склону, где отложения субстрата имеют консистенцию, допускающую эрозию водным источником. Однако происходит нечто более фундаментальное. Меандры образуются на ледниках, где нет наносов. Меандры образуются, когда вода стекает по оконному стеклу автомобиля. Меандры образуются в открытом океане; Гольфстрим проходит через более статичные воды Атлантики по схеме, имеющей ту же геометрию, что и меандр. Научная мысль соглашается, что энергия играет роль в формировании меандров. Чтобы понять, как это может быть, необходимо посмотреть на форму меандрирующей излучины и параметры прибрежной системы, к которой она принадлежит.

Леопольд Луна был главным гидрологом Геологической службы США и считается одним из ведущих авторитетов в области потамологии в Северной Америке. Он был внимательным наблюдателем за реками, выполняя полевые измерения и выводя математические соотношения, которые количественно определяли поведение рек. Он отметил, что извилистые реки имеют заметно сходные размеры, что длина волны изгиба примерно в 10 раз больше ширины w и примерно в 5 раз больше радиуса кривизны rc; отношение радиуса кривизны к ширине, таким образом, было примерно 2 к 1. Луна вычислила w/rc для 50 рек и обнаружила, что они очень похожи, что объясняет, почему извилистые реки выглядят примерно одинаково на планиметрических картах. Это означает, что более широкая река изгибается намного меньше, явление, которое также было отмечено Эйнштейном, который объяснил это более медленным спиральным течением, которое меньше размывает берега. Это также важно для понятия количества энергии в потоке.

Форма меандра характерна; это не сегмент круга и не обычная синусоидальная волна. Луна назвала эту форму синусоидальной кривой. Чтобы понять это, представьте себя в лодке на реке (без мандариновых деревьев и мармеладного неба) с компасом в одной руке. Двигаясь вниз по извилистой реке, периодически считывая показания компаса, вы обнаружите, что ваше направление (угол курса ψ) будет меняться в зависимости от синуса пройденного вами расстояния, или, говоря математическим языком:0003

                                              угол курса ψ = csin(s)

Где s — расстояние вниз по реке (в радианах), а c — константа, зависящая от максимального угла, который изгиб меандра образует с осью вниз по реке. Это зависит от ряда факторов, включая топографию и течение реки; значение меньше единицы дает слегка волнистый поток, а значение около двух дает более характерный меандр в форме подковы.

Синусоидальная кривая имеет три свойства, которые дают некоторое представление о причине изгиба рек: это путь минимального изгибающего напряжения, путь минимальной дисперсии направления и путь, представляющий наиболее вероятное случайное блуждание. То, что кривая, образованная синусоидой, является фундаментальным свойством физики, можно продемонстрировать на примере стальной полосы, которая, если ее закрепить с обоих концов и изогнуть в виде дуги, примет характерную форму подковы. С математической точки зрения минимизация напряжения изгиба связана с тем, что это напряжение пропорционально квадрату кривизны в каждой точке; это имеет логическую привлекательность. Кривизна определяется как величина, обратная радиусу кривизны, так что изгиб с малым радиусом имеет большую кривизну и, следовательно, большее напряжение. Поскольку сумма квадратов кривизны в каждой точке синусоидальной кривой минимальна, то и напряжение изгиба минимально. Направленная дисперсия имеет аналогичное происхождение.

Случайное блуждание немного сложнее объяснить, но оно важно тем, что оно необходимо, хотя и недостаточно, для понимания кажущейся случайности речных меандров. Основная идея проста. Человек (или молекула воды) стартует в точке a, взлетает под случайным углом с длиной шага L, повторяя процесс с новым углом, но с той же длиной шага, пока не будет достигнута конечная точка b. Если затем попытаться определить, какие из этих случайных блужданий наиболее часты, окажется, что блуждания, взятые из нормального распределения вероятностей (также известного как гауссовское по имени немецкого математика Фредерика Гаусса), дают нетривиальное решение. Хотя фактическое решение не определено, кривая, построенная по синусоиде, является близким приближением. На макроскопическом уровне извилистости реки разница буквально теряется в водорослях.